
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое знакомство с перегрузкой функций ⇐ ПредыдущаяСтр 3 из 3
Перегрузка функций позволяет вашим программам определять несколько функций с одним и тем же именем и типом возвращаемого значения. Например, следующая программа перегружает функцию с именем add_values. Первое определение функции складывает два значения типа int. Второе определение функции складывает три значения. В процессе компиляции C++ корректно определяет функцию, которую необходимо использовать: #include <iostream.h> int add_values(int a,int b) { int add_values (int a, int b, int c) ( void main(void) { Как видите, программа определяет две функции с именами add_values Первая функция складывает два значения типа int, в то время как вторая складывает три значения. Вы не обязаны что-либо предпринимать специально для того, чтобы предупредить компилятор о перегрузке, просто используйте ее. Компилятор разгадает, какую функцию следует использовать, основываясь на предлагаемых программой параметрах. Подобным образом следующая программа MSG_OVR.CPP перегружает функцию show_message. Первая функция с именем show_message выводит стандартное сообщение, параметры ей не передаются. Вторая выводит передаваемое ей сообщение, а третья выводит два сообщения: #include <iostream.h> void show_message(void) { void show_message(char *message) { void show_message(char *first, char *second) { void main(void) { КОГДА НЕОБХОДИМА ПЕРЕГРУЗКА Одним из наиболее общих случаев использования перегрузки является применение функции для получения определенного результата, исходя из различных параметров. Например, предположим, что в вашей программе есть функция с именем day_of_week, которая возвращает текущий день недели (0 для воскресенья, 1 для понедельника,..., 6 для субботы). Ваша программа могла бы перегрузить эту функцию таким образом, чтобы она верно возвращала день недели, если ей передан юлианский день в качестве параметра, или если ей переданы день, месяц и год: int day_of_week(int julian_day) {
int day_of_week(int month, int day, int year) { По мере изучения объектно-ориентированного программирования в C++, представленного в следующих уроках, вы будете использовать перегрузку функций для расширения возможностей своих программ. Перегрузка функций улучшает удобочитаемость программ Перегрузка функций C++ позволяет вашим программам определять несколько функций с одним и тем же именем. Перегруженные функции должны возвращать значения одинакового типа*, но могут отличаться количеством и типом параметров. До появления перегрузки функций в C++ программисты языка С должны были создавать несколько функций с почти одинаковыми именами. К сожалению программисты, желающие использовать такие функции, должны были помнить, какая комбинация параметров соответствует какой функции. С другой стороны, перегрузка функций упрощает задачу программистов, требуя, чтобы они помнили только одно имя функции. * Перегруженные функции не обязаны возвращать значения одинакового типа по той причине, что компилятор однозначно идентифицирует функцию по ее имени и набору ее аргументов. Для компилятора функции с одинаковыми именами, но различными типами аргументов — разные функции, поэтому тип возвращаемого значения — прерогатива каждой функции. — Прим.перев. ЧТО ВАМ НЕОБХОДИМО ЗНАТЬ Перегрузка функций позволяет вам указать несколько определений для одной и той же функции. В процессе компиляции C++ определит, какую функцию следует использовать, основываясь на количестве и типе передаваемых параметров. Из данного урока вы узнали, что перегружать функции достаточно просто. Из урока 14 вы узнаете, как ссылки C++ упрощают процесс изменения параметров внутри функций. Однако, прежде чем перейти к уроку 14, убедитесь, что вы изучили следующие основные концепции:
№25
Рекурсия Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Вообще, рекурсивным называется любой объект, который частично определяется через себя. Например, приведенное ниже определение двоичного кода является рекурсивным: <двоичный код>::= <двоичная цифра> | <двоичный код><двоичная цифра> <двоичная цифра>::= 0 | 1Здесь для описания понятия были использованы, так называемые, металингвистический формулы Бэкуса-Наура (язык БНФ); знак "::=" обозначает "по определению есть", знак "|" — "или". Вообще, в рекурсивном определении должно присутствовать ограничение, граничное условие, при выходе на которое дальнейшая инициация рекурсивных обращений прекращается. Приведём другие примеры рекурсивных определений. Пример 1. Классический пример, без которого не обходятся ни в одном рассказе о рекурсии, — определение факториала. С одной стороны, факториал определяется так: n!=1*2*3*...* n. С другой стороны,
Граничным условием в данном случае является n <=1. Пример 2. Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n:
Задание. По аналогии определите функцию S(n), вычисляющую сумму цифр заданного натурального числа. Пример 3. Функция C(m, n), где 0 <= m <= n, для вычисления биномиального коэффициента Ниже будут приведены программные реализации всех этих (и не только) примеров. Обращение к рекурсивной подпрограмме ничем не отличается от вызова любой другой подпрограммы. При этом при каждом новом рекурсивном обращении в памяти создаётся новая копия подпрограммы со всеми локальными переменными. Такие копии будут порождаться до выхода на граничное условие. Очевидно, в случае отсутствия граничного условия, неограниченный рост числа таких копий приведёт к аварийному завершению программы за счёт переполнения стека. Порождение все новых копий рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Максимальное количество копий рекурсивной подпрограммы, которое одновременно может находиться в памяти компьютера, называется глубиной рекурсии. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным подъёмом. Выполнение действий в рекурсивной подпрограмме может быть организовано одним из вариантов: { { { P; операторы; операторы; операторы; P; P; } } операторы; } рекурсивный подъём рекурсивный спуск и рекурсивный спуск, и рекурсивный подъёмЗдесь P — рекурсивная подпрограмма. Как видно из рисунка, действия могут выполняться либо на одном из этапов рекурсивного обращения, либо на обоих сразу. Способ организации действий диктуется логикой разрабатываемого алгоритма. Реализуем приведённые выше рекурсивные определения в виде функций. Пример 1. double Factorial(int N) { double F; if (N<=1) F=1.; else F=Factorial(N-1)*N; return F; }Пример 2.
Пример 3. int C(int m, int n) { int f; if (m==0||m==n) f=1; else f=C(m, n-1)+C(m-1, n-1); return f; }Пример 4. Вычислить сумму элементов линейного массива. При решении задачи используем следующее соображение: сумма равна нулю, если количество элементов равно нулю, и сумме всех предыдущих элементов плюс последний, если количество элементов не равно нулю. #include <stdio.h> #include <conio.h> #include <stdlib.h> #include <time.h> int summa(int N, int a[100]); int i,n, a[100]; void main() { clrscr(); printf("\nКоличество элементов массива? "); scanf("%d", &n); printf("\nВ сформированном массиве %d чисел:\n", n); randomize(); for (i=0; i<n; i++) {a[i]= -10+random(21); printf("%d ", a[i]);} printf("Сумма: %d", summa(n-1, a)); } int summa(int N, int a[100]) { if (N==0) return a[0]; else return a[N]+summa(N-1, a); }
Пример 5. Определить, является ли заданная строка палиндромом, т.е. читается одинаково слева направо и справа налево. Идея решения заключается в просмотре строки одновременно слева направо и справа налево и сравнении соответствующих символов. Если в какой-то момент символы не совпадают, делается вывод о том, что строка не является палиндромом, если же удается достичь середины строки и при этом все соответствующие символы совпали, то строка является палиндромом. Граничное условие — строка является палиндромом, если она пустая или состоит из одного символа. #include <stdio.h> #include <conio.h> #include <string.h> char s[100]; int pal(char s[100]); void main() { clrscr(); printf("\nВведите строку: "); gets(s); if (pal(s)) printf("Строка является палиндромом"); else printf("Строка не является палиндромом"); } int pal(char s[100]) { int l; char s1[100]; if (strlen(s)<=1) return 1; else {l=s[0]==s[strlen(s)-1]; strncpy(s1, s+1, strlen(s)-2); s1[strlen(s)-2]='\0'; return l&&pal(s1);} }
Подводя итог, заметим, что использование рекурсии является красивым приёмом программирования. В то же время в большинстве практических задач этот приём неэффективен с точки зрения расходования таких ресурсов ЭВМ, как память и время исполнения программы. Использование рекурсии увеличивает время исполнения программы и зачастую требует значительного объёма памяти для хранения копий подпрограммы на рекурсивном спуске. Поэтому на практике разумно заменять рекурсивные алгоритмы на итеративные.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.163.31 (0.011 с.) |
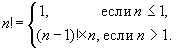

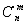 по следующей формуле
по следующей формуле  является рекурсивной.
является рекурсивной.


