
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 7 2.2. Координатные и импульсные состояния поля
Определим операторы безразмерных координат
Операторы размерных координат и импульсов удобно представить в виде
Заметим, что, поскольку операторы уничтожения и рождения фотонов являются эрмитовски-сопряженными, операторы обобщенной координаты и импульса являются самосопряженными (эрмитовыми), как это следует из их определения (2.40) –– (2.43). Известно, что собственные значения эрмитовых операторов являются действительными числами, а их собственные функции взаимно ортогональны. С другой стороны, наблюдаемым физическим величинам в квантовой механике как раз соответствуют эрмитовы операторы. Так что в отличие от неэрмитовых операторов уничтожения и рождения фотонов операторам обобщенной координаты и обобщенного импульса электромагнитного поля должны соответствовать наблюдаемые характеристики поля. Действительно, если рассматривать разложение электромагнитного поля не на бегущие волны, как это представлено выражением (2.1), а на стоячие волны, то напряженности электрического и магнитного поля пространственных гармоник могут быть выражены через обобщенные координаты и импульсы:
В формулах (2.44), (2.45) для простоты приведены скалярные напряженности поля, Размерность обобщенных координат и импульсов поля не совпадает с размерностью координаты и импульса вещественного осциллятора с отличной от нуля массой. В гауссовой системе единиц для соответствующих размерностей имеем:
Пользуясь формулами (2.40) –– (2.41), имеем следующие выражения для операторов уничтожения и рождения фотонов через операторы безразмерных обобщенных координат и импульсов:
Из этих формул видна эрмитовская сопряженность операторов Из определений (2.40) –– (2.41) и коммутационных соотношений (2.20) –– (2.21) следует выражение для коммутаторов операторов
Отсюда с учетом (2.42) –– (2.43) коммутатор размерных обобщенной координаты и импульса равен
Явный вид операторов обобщенной координаты и импульса зависит от конкретного представления вектора состояния квантовой системы, т.е. от того, какая из величин выбрана в качестве аргумента (независимой переменной) при явной записи вектора состояния. Так, в случае
Введем в рассмотрение координатные
Координатные и импульсные состояния электромагнитного поля образуют полный набор ортогональных базисных функций, по которым может быть разложен произвольный вектор состояния электромагнитного поля. В отличие от энергетических состояний, принадлежащих (в случае электромагнитного поля) дискретному спектру, собственные значения координатных и импульсных состояний пробегают непрерывный ряд числовых значений и соответствующие собственные векторы образуют непрерывный спектр. Явный вид координатного вектора-состояния электромагнитного поля в
Поясним обозначение данного вектора состояния (левая часть равенства (2.54)). Буква
Заметим, что в правой части равенства (2.55) стоит дельта-функция, в отличие от символа Кроннекера в случае нормировки энергетических состояний (2.15). Это обстоятельство связано с непрерывным спектром импульсных состояний. Вероятность обнаружить значение обобщенной координаты, равное
подставляя в которую явный вид вектора импульсного состояния (2.54), находим
т.е. соответствующая вероятность равномерно «размазана» по всему спектру возможных значений обобщенной координаты. Другим словами, в импульсном состоянии, когда значение обобщенного импульса фиксировано, значение обобщенной координаты полностью неопределено. Точно так же в координатном состоянии значение обобщенного импульса полностью неопределено, а вероятность дается правой частью равенства (2.57). Эти обстоятельства являются отражением общего квантово-механического принципа неопределенности Гейзенберга, который может быть представлен следующим неравенством:
где
Из выражений (2.58) –– (2.59) следует, что если коммутатор операторов двух физических величин равен нулю, то соответствующие величины могут быть одновременно определены сколь угодно точно. Если же этот коммутатор отличен от нуля, то чем точнее будет определена одна из величин, тем менее точно будет определена другая величина. В частности, для обобщенной координаты и импульса условие (2.58) дает
При записи (2.60) было использовано значение коммутатора (2.50). Постоянная Планка явно выделена в формулах (2.58) ––(2.59), чтобы обозначить масштаб квантово-механической неопределенности. Выразим гамильтониан электромагнитного поля через операторы обобщенных координат и импульсов. С этой целью подставим в формулу (2.26) правые части равенств (2.47) –– (2.48), в результате получим
При выводе этой формулы было использовано коммутационное соотношение (2.49), в результате чего исчезло слагаемое ½, стоящее в круглых скобках правых частей равенства (2.26). Переходя в формуле (2.61) к размерным операторам обобщенных координат и импульсов, окончательно находим
Полученное выражение представляет гамильтониан электромагнитного поля в виде суммы гамильтонианов радиационных осцилляторов, соответствующих различным модам поля. Если в формуле (2.62) перейти от операторных величин к обычным (с -числовым) функциям, то получим классическую функцию Гамильтона электромагнитного поля в виде
Функция Гамильтона (2.63) описывает набор гармонических осцилляторов с равной единице массой. Уравнения Гамильтона с функцией (2.63) дают
Точка над символами обобщенных координат и импульсов в левых частях формул (2.64) –– (2.65) обозначает дифференцирование по времени. Равенство (2.64) представляет собой уравнение движения гармонического осциллятора, а формула (2.65) является выражением для обобщенного импульса осциллятора с массой, равной единице. Отметим, что уравнения (2.64) –– (2.65) справедливы также в операторном виде, если ввести зависящие от времени (гейзенберговские) операторы обобщенных координат и импульсов по формулам:
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.144.40 (0.01 с.) |
 и импульсов
и импульсов  электромагнитного поля с помощью операторов уничтожения и рождения фотонов в соответствии с формулами:
электромагнитного поля с помощью операторов уничтожения и рождения фотонов в соответствии с формулами: , (2.40)
, (2.40) . (2.41)
. (2.41) , (2.42)
, (2.42) . (2.43)
. (2.43) , (2.44)
, (2.44) . (2.45)
. (2.45) –– объем квантования.
–– объем квантования. ;
;  . (2.46)
. (2.46) , (2.47)
, (2.47) . (2.48)
. (2.48) и
и  .
. . (2.49)
. (2.49) . (2.50)
. (2.50) - представления операторы обобщенной координаты и импульса электромагнитного поля имеют вид
- представления операторы обобщенной координаты и импульса электромагнитного поля имеют вид ,
,  . (2.51)
. (2.51) и импульсные
и импульсные  состояния электромагнитного поля. Эти состояния являются собственными векторами соответственно оператора координаты и оператора импульса, т.е. удовлетворяют следующим уравнениям:
состояния электромагнитного поля. Эти состояния являются собственными векторами соответственно оператора координаты и оператора импульса, т.е. удовлетворяют следующим уравнениям: , (2.52)
, (2.52)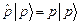 . (2.53)
. (2.53) . (2.54)
. (2.54) под знаком кет-вектора (правые угловые скобки) обозначают тип состояния (импульсное), а буква
под знаком кет-вектора (правые угловые скобки) обозначают тип состояния (импульсное), а буква  . (2.55)
. (2.55) , (2.56)
, (2.56) , (2.57)
, (2.57) , (2.58)
, (2.58) и
и  –– квантово-механические неопределенности физических величин
–– квантово-механические неопределенности физических величин  и
и  , которым соответствуют операторы
, которым соответствуют операторы  и
и  .
.  –– действительное неотрицательное число, связанное с коммутатором рассматриваемых величин согласно равенству
–– действительное неотрицательное число, связанное с коммутатором рассматриваемых величин согласно равенству . (2.59)
. (2.59) . (2.60)
. (2.60) . (2.61)
. (2.61) . (2.62)
. (2.62) . (2.63)
. (2.63) , (2.64)
, (2.64) . (2.65)
. (2.65) ,
,  . (2.66)
. (2.66)


