Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информационная оценка неопределенности и энтропия как мера неопределенностиСтр 1 из 2Следующая ⇒
Выше отмечалось, что в информационном смысле вероятность может трактоваться как степень неопределенности наших знаний о наступлении случайных событий, т.е. вероятность наступления события трактуется трактуется как неопределенность имеющейся информации о событии. Дополнительные данные (информация) влияют на уровень наших знаний и это может изменить неопределенность нашей оценки вероятности, т.е. факт получения информации всегда связан с уменьшением неопределенности выбора решения. Таким образом, делаем вывод: информация – это то, что помогает принимать решение. Задача получения количественной меры для оценки неопределенности информации впервые была решена Клодом Шенноном в его знаменитой статье «Математическая теория связи». Утверждалось, что самым важным результатом получения информации является устранение (уменьшение) степени неопределенности, и что для нахождения количественной меры неопределенности информации можно использовать несколько априорных предположений об источнике информации самого общего характера: 1. Источник информации (например, некоторый опыт – эксперимент по измерению скорости частиц) в каждый момент времени (каждый исход опыта) случайным образом может принять одно из множества состояний (исходов опыта). Поскольку одни состояния источника (одни исходы опыта) реализуются чаще других, то каждому из них ставится в соответствие некоторая вероятность, совокупность которых будет характеризовать источник информации (результаты опытов). При этом неопределенность информации относительно всех исходов опыта должна зависеть от вероятности, приписываемой каждому исходу. Если pi – вероятность i-го исхода, а общее количество возможных исходов n, то неопределенность U должна быть функцией всех pi, т.е. 2. Если все исходы равновероятны, т.е. 3. Если два независимых друг от друга опыта А и В (т.е. два независимых источника информации с числом равновероятных состояний А и В) рассматривать как один сложный опыт, состоящий из А и В (один общий источник информации реализует одновременно эту пару состояний), то естественно предположить, что неопределенность объединенного источника должна равняться сумме неопределенностей исходных источников. Поскольку общее число возможных состояний объединенного источника равно АВ, то искомая мера его неопределенности должна удовлетворять условию
4. Конечное решение задачи не должно зависеть от значений промежуточных результатов, т.е. если рассматривать m вариантов решений, на каждом их которых возможно Х вариантов исходов опытов, то общее количество возможных равновероятных исходов будет равно Т.к.
Поскольку при равновероятных исходах Если в результате опыта мы получили другое значение вероятности
В случае, когда Дело в том, что формально структура этого выражения совпадает со структурой выражения для энтропии физической системы, полученной ранее Больцманом. Так, согласно второму закону термодинамики энтропия S замкнутой системы определяется выражением:
где Совпадение формул Л. Больцмана и К. Шеннона имеет глубокий физический смысл, характеризуя степень разнообразия системы, а сами энтропии имеют одинаковые свойства, например, достигают максимума значения в равновесном, наиболее вероятном, состоянии системы. Если рассматривать число способов размещения А=1/P, т.е. число всех возможных состояний системы, то S=k lnA, где А – термодинамическая вероятность. {Фазовое пространство Модели классического и квантового идеального газа. Этих тем не было в рукописях, которые мы обрабатывали - смотрите свои конспекты} Проблема различимости N частиц.
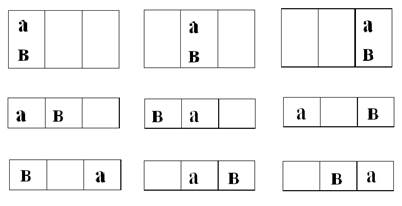
Эта проблема не возникает в классической физике, т.к. даже в модели идеального газа, состоящего из тождественных частиц, их различимость обусловлена теоретической возможностью одновременной локализации (т.е. точного определения положения и скорости) частицы в пространстве координат и импульсов, т.е. возможностью представить состояние каждой частицы фазовой точкой в μ – пространстве. В квантовой физике тождественные частицы неотличимы друг от друга, так как за их движением нельзя следить одновременно во времени вследствие принципа неопределенности Гейзенберга. Система описывается волновой функцией, которая согласно принципу запрета Паули должна быть либо симметрично относительно перестановки (транспозиции) переменных любых двух частиц (для бозонов, частиц с целым спином – фотонов, π- и к- мезонов и др.), либо антисимметрична относительно той же операции(для фермионов, частиц с полуцелым спином – электронов, позитронов, протонов, нейтронов, μ – мезонов, гиперонов и др.) Сложные частицы(ядра, атомы, ионы, молекулы), состоящие только из частиц со спином = 1/2, будут относится к бозонам, если число элементарных частиц в них четное, либо к фермионам, если оно не четное. Иллюстрацией различий в статистических свойствах различных частиц, фермионов и бозонов, может служить простой пример. Пусть нам надо разместить две частицы по трем ячейкам. Если эти частицы различимы (обозначим их в этом случае а и в) и полностью независимы друг от друга типа классических, то возможны девять различных размещений (рис. 4). Если они не различимы, но независимы друг от друга (бозоны), т.е. могут находится в одном состоянии одновременно, по принципу запрета Паули, то возможны шесть различных размещений (рис.5) (где различимые частицы изображены крестиками). Если же они неразличимы и зависимы друг от друга, т.е. не могут находиться в одном состоянии одновременно по принципу Паули (фермионы), то возможны всего три варианта размещения (рис.6).
Рис. 4. Классические частицы
Рис.5. Бозоны
Рис.5. Фермионы
Распределение Максвелла- Больцмана в квазиквантовом приближении. Переходя к классическому идеальному газу, т.е. считая, что все тождественные частицы различимы, рассмотрим ту же задачу о размещении в i- ячейке с энергией Ei и числом ячеек ri, Ni различимых частиц.
Общее число способов Wi какими можно разместить все N частиц по всем i ящикам всей системы, не фиксируя ячейки, в которые они при этом попадают, определяется тем, что для различимых частиц разные способы их размещения отличаются друг от друга только перестановками частиц, находящихся в разных ячейках, без учета несущественных, не дающих новых результатов, перестановок частиц внутри каждого ящика. Поскольку полное число перестановок N частиц составит N!, а число несущественных перестановок внутри каждого ящика i с числом частиц Ni будет равно Ni!, при их общем количестве по всем ящикам, равном Пi (Ni!), то Wi = Так как для каждого из Ni частиц внутри каждого i ящика существует ri возможностей размещения по ячейкам этого ящика, общее число размещений всех Ni частиц по этим ri ячейкам составит (ri)Ni,а для всех ящиков будет равно Пi (ri)Ni Поэтому полное число способов размещений N частиц по всем ячейкам, всех ящиков составил: W= Wi* Пi (ri)Ni = Пользуясь формулой Стирлинга
Получим
Частицы размещаются по ячейкам
Этот вид распределения Максвелла, привязан к числу ячеек в ящике.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.120 (0.05 с.) |
 .
. , то неопределенность U должна быть монотонно возрастающей функцией n (числа возможных исходов), т.е.
, то неопределенность U должна быть монотонно возрастающей функцией n (числа возможных исходов), т.е. 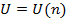 .
. . Сразу отметим, что этому условию отвечает U
. Сразу отметим, что этому условию отвечает U  . Основание log не имеет принципиального значения и определяет только масштаб или единицу неопределенности. Если за основание взять 2 (2возможных состояния), то единицей измерения неопределенности будет двоичная единица или бит; основание 10, следовательно, неопределенность в десятичных единицах, дитах. В статистической физике пользуются натуральным логарифмом с основанием е.
. Основание log не имеет принципиального значения и определяет только масштаб или единицу неопределенности. Если за основание взять 2 (2возможных состояния), то единицей измерения неопределенности будет двоичная единица или бит; основание 10, следовательно, неопределенность в десятичных единицах, дитах. В статистической физике пользуются натуральным логарифмом с основанием е. . В силу предположения 2, должно соблюдаться
. В силу предположения 2, должно соблюдаться 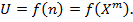 Кроме того, поскольку, в силу предположения 3, общая неопределенность этих
Кроме того, поскольку, в силу предположения 3, общая неопределенность этих  исходов должна равняться сумме неопределенностей
исходов должна равняться сумме неопределенностей  по каждому из m вариантов опытов, т.е.
по каждому из m вариантов опытов, т.е.  . Это тоже приводит к
. Это тоже приводит к 

 есть вероятность, приписываемая каждому исходу, то для неопределенности исхода можно записать
есть вероятность, приписываемая каждому исходу, то для неопределенности исхода можно записать  – формула Шеннона для оценки неопределенности равновероятных исходов.
– формула Шеннона для оценки неопределенности равновероятных исходов. , то неопределенность оценки исходов изменится и станет равной
, то неопределенность оценки исходов изменится и станет равной  . Разность оценок неопределенности до и после опыта есть информация, полученная в опыте:
. Разность оценок неопределенности до и после опыта есть информация, полученная в опыте: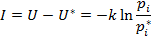
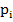 варьируется (т.е. для неравновероятных исходов), для оценки ожидаемого объема неопределенности используется среднее значение (математическое ожидание), по определению среднего, равное:
варьируется (т.е. для неравновероятных исходов), для оценки ожидаемого объема неопределенности используется среднее значение (математическое ожидание), по определению среднего, равное:  Это и есть знаменитая формула К. Шеннона, которую математически строго доказал Л. Хинчин. Величину
Это и есть знаменитая формула К. Шеннона, которую математически строго доказал Л. Хинчин. Величину  по предложению Нернста стали называть информационной энтропией, что совсем неслучайно.
по предложению Нернста стали называть информационной энтропией, что совсем неслучайно. 

 - полное число молекул в системе,
- полное число молекул в системе,  - число молекул, обладающих скоростью Vi. Т.к.
- число молекул, обладающих скоростью Vi. Т.к. 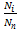 есть вероятность того, что молекула
есть вероятность того, что молекула  .
.


 ;
; Пi
Пi