
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еквіпотенціальні поверхні. Градієнт потенціалу
Оскільки електростатичне поле характеризується скалярною безперервною функцією – потенціалом, то в просторі завжди можна виділити геометричне місце точок з рівними потенціалами. В тривимірному просторі така сукупність точок являє собою поверхню, яку прийнято називати еквіпотенційною. Тому електростатичне поле може бути зображено безліччю еквіпотенціальних поверхонь. Щоб з’ясувати положення цих поверхонь, а також їх орієнтацію відносно силових ліній  , запроваджуємо поняття градієнта потенціалу – важливу характеристику поля, яка визначає зв'язок між , запроваджуємо поняття градієнта потенціалу – важливу характеристику поля, яка визначає зв'язок між  та та 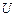 . Як відомо з математики, в загальному випадку градієнт – це вектор, який характеризує просторову швидкість зміни скалярної величини і напрямлений в бік її збільшення. Тому градієнт потенціалу . Як відомо з математики, в загальному випадку градієнт – це вектор, який характеризує просторову швидкість зміни скалярної величини і напрямлений в бік її збільшення. Тому градієнт потенціалу 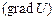 електростатичного поля – це вектор, за модулем рівний швидкості зміни потенціалу і напрямлений в бік його найшвидшого зростання. Тепер неважко уявити, що, оскільки найшвидша зміна потенціалу відповідає найкоротшій відстані між еквіпотенціальними поверхнями електростатичного поля – це вектор, за модулем рівний швидкості зміни потенціалу і напрямлений в бік його найшвидшого зростання. Тепер неважко уявити, що, оскільки найшвидша зміна потенціалу відповідає найкоротшій відстані між еквіпотенціальними поверхнями  (рис.1.6), то вектор (рис.1.6), то вектор 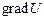 перпендикулярний дотичній еквіпотенціальної поверхні в конкретній точці і напрямлений в бік поверхні з більшим потенціалом. Відповідно визначенню градієнт потенціалу можна записати так: перпендикулярний дотичній еквіпотенціальної поверхні в конкретній точці і напрямлений в бік поверхні з більшим потенціалом. Відповідно визначенню градієнт потенціалу можна записати так:
де Прирости відстаней
Відношення приросту потенціалу
а в нескінченно малих величинах це є похідною за напрямком
Останнє співвідношення визначає проекцію вектора
Таким чином, якщо замість напрямку
або
Відповідно до виразу (1.16) модуль вектора
Для визначення зв'язку напруженості поля
При порівнянні виразів (1.16) і (1.19) одержимо загальне співвідношення:
Це співвідношення свідчить про те, що вектор напруженості поля
На початку попереднього підрозділу відзначалося, що для розв'язування прямої задачі електростатики рівності Гауса–Остроградського в диференціальній формі було недостатньо. Тепер на основі одержаних співвідношень (1.12) – (1.20) можна створити передумови для розв’язку прямої задачі електростатики –знаход-ження характеристик поля за заданим розподілом зарядів.
Рівняння Пуассона–Лапласа Розв'язання прямої задачі є неможливим до тих пір, поки не визначені три невідомі проекції вектора
Підставляючи ці співвідношення у вираз (1.10), одержимо:
або в загальному випадку, змінюючи у виразі (1.18)
Співвідношення (1.22) є загальною формою запису рівняння Пуассона, а (1.21) - рівняння Пуассона в прямокутній системі координат. З курсу математики відомий розв’язок рівняння Пуассона у вигляді об'ємного інтегралу:
де Якщо в області простору, який розглядається, заряди відсутні, то рівняння (1.21) і (1.22) набувають вигляду:
Рівняння (1.24) або (1.25) називаються рівнянням Лапласа. Вони застосуються для розрахунку полів в області простору, вільної від зарядів. Розв'язування рівняння Лапласа здійснюють у такій послідовності. Представимо розв’язок (1.24) у вигляді добутку, в якому кожний співмножник є функцією лише однієї змінної:
Підставимо цей умовний розв'язок в початкове рівняння (1.24):
Перетворимо одержаний вираз таким чином, щоб кожний додаток в ньому залежав від однієї змінної:
Співвідношення (1.27) є рівнянням з трьома невідомими. Природно, що воно має розв’язок тільки при наявності еквівалентної системи з трьох рівнянь. Тому доцільно припустити, що рівняння (1.27) має розв'язок лише при умові, що кожний доданок, що входить в нього, є постійною величиною. Для одержання еквівалентної системи з трьох рівнянь, кожне з яких є функцією тільки однієї змінної, виконаємо такі дії.
Диференціюємо вираз (1.27) за змінною Диференціюємо вираз (1.27) по
Таким чином, одержана система з трьох рівнянь, кожне з яких має лише одну невідому. Перепишемо перше рівняння цієї системи з урахуванням виразу (1.27) у вигляді:
та помножимо його на
Розв’язок цього стандартного рівняння здійснюється у показникових функціях. Приведемо одержане рівняння до такої канонічної форми, при якій його розв'язок виявляється через гармонічні функції. Оскільки позначення
Його розв'язок буде таким:
В співвідношенні (1.28) Аналогічно записуємо інші рівності отриманої системи:
та їх розв'язки:
де Підставимо вирази (1.28), (1.29) і (1.30) в (1.26) та розв'яжемо рівняння Лапласа. Для цього із введених коефіцієнтів два будемо вибирати довільно, тоді третій буде зв'язаний з цим вибором. Нехай
або:
Ця уявна величина входить в аргументи тригонометричних функцій - синуса та косинуса. Тоді розв'язок (1.30) записується через гіперболічні косинус та синус:
Надалі виникає проблема визначення коефіцієнтів А 1, А 2, В 1, В 2, С 1, С 2, які відповідають єдиному розв'язку рівняння Лапласа. При цьому необхідно розглянути поведінку вектора напруженості електростатичного поля при переході через поверхню розподілу двох середовищ. Єдиному розв'язку конкретної задачі буде відповідати такий розв'язок рівняння Лапласа із безлічі інших його розв'язків, який водночас задовольняє як самому рівнянню, так і деяким граничним умовам, які існують на поверхні розподілу двох середовищ.
1.9. Граничні умови електростатики
Якщо силові лінії векторів 1.9.1. Граничні умови для тангенційних складових вектора
Це означає, що сума робіт по кожній із сторін контуру:
Cпрямовуємо до нуля довжини сторін
В цьому співвідношенні перший доданок характеризує
де
або, враховуючи, що
Тут замість знака плюс з'явився знак мінус внаслідок того, що
або:
тобто тангенційні (дотичні) складові вектора 1.9.2. Граничні умови для нормальних складових вектора Нехай вектор
де
Побудуємо циліндричну поверхню, що перерізує поверхню поділу двох середовищ (рис. 1.8).
Нехай площа поперечного перетину циліндра –
Оскільки заряд зосереджений на поверхні
оскільки
або, скорочуючи на величину
де перший доданок – нормальна складова
Вираз (1.32) свідчить про те, що нормальні (перпендикулярні) складові вектора
Очевидно, що при Отже, на границі поділу двох середовищ тангенційні складові силових ліній
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.193.172 (0.05 с.) |

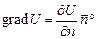 ,
,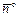 – одиничний вектор уздовж нормалі
– одиничний вектор уздовж нормалі  . Для визначення градієнта потенціалу в прямокутній системі координат розглянемо спочатку похідну потенціалу
. Для визначення градієнта потенціалу в прямокутній системі координат розглянемо спочатку похідну потенціалу  здовж довільного напряму
здовж довільного напряму 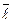 .
.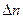 і
і 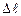 (рис.1.6) зв'язані між собою очевидним співвідношенням:
(рис.1.6) зв'язані між собою очевидним співвідношенням: .
.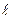
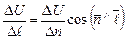 ,
, .
. на довільний напрям
на довільний напрям  . (1.16)
. (1.16) ,
,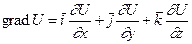 . (1.17)
. (1.17) :
: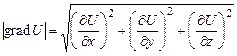 . (1.18)
. (1.18) в границі:
в границі: . (1.19)
. (1.19)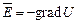 . (1.20)
. (1.20)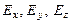 .Так, одержавши додаткові відомості про характеристики поля у вигляді співвідношень (1.16) – (1.20), можна обчислити проекції вектора
.Так, одержавши додаткові відомості про характеристики поля у вигляді співвідношень (1.16) – (1.20), можна обчислити проекції вектора  ;
; 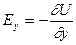 ;
; 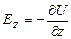 .
.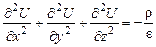 (1.21)
(1.21)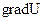 зі знаком мінус, отримаємо:
зі знаком мінус, отримаємо: . (1.22)
. (1.22)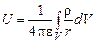 , (1.23)
, (1.23)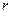 – відстань між елементом
– відстань між елементом  та точкою нагляду. Далі за відомим потенціалом
та точкою нагляду. Далі за відомим потенціалом 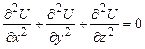 , (1.24)
, (1.24) . (1.25)
. (1.25) . (1.26)
. (1.26)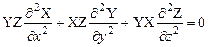 .
.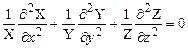 . (1.27)
. (1.27) . Бачимо, що отриманий диференціал дорівнює нулю. Це означає, що перший доданок у (1.27) є сталою величиною. Позначимо її через
. Бачимо, що отриманий диференціал дорівнює нулю. Це означає, що перший доданок у (1.27) є сталою величиною. Позначимо її через 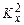 .
. та
та 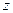 . За результатами зробимо висновки про те, що інші доданки у (1.27) теж сталі величини, наприклад,
. За результатами зробимо висновки про те, що інші доданки у (1.27) теж сталі величини, наприклад,  та
та 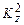 . Вони, відповідно до виразу (1.27), зв'язані рівністю:
. Вони, відповідно до виразу (1.27), зв'язані рівністю: .
.
 :
: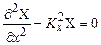 .
. введені довільно, то змінимо їх знаки на обернені. Тоді останнє рівняння набуде вигляду:
введені довільно, то змінимо їх знаки на обернені. Тоді останнє рівняння набуде вигляду: .
. . (1.28)
. (1.28)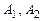 – деякі сталі.
– деякі сталі. ,
, ,
, , (1.29)
, (1.29)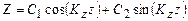 , (1.30)
, (1.30)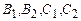 – відповідні сталі.
– відповідні сталі.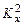 та
та 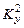 – позитивні натуральні числа. Тоді:
– позитивні натуральні числа. Тоді: ,
,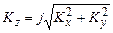 .
.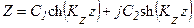 .
. перетинають границю розподілу двох середовищ з різними значеннями
перетинають границю розподілу двох середовищ з різними значеннями  , то
, то  і
і  , тангенціальних складових
, тангенціальних складових  і
і  , а також потенціалу
, а також потенціалу 
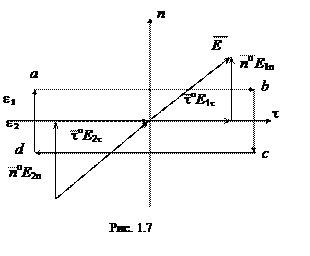 Нехай силова лінія
Нехай силова лінія  та
та  (рис.1.7). Графічне зобра-ження
(рис.1.7). Графічне зобра-ження 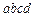 , сторони якого нескінченно малі, а напрямок його обходу - за годинниковою стрілкою. Циркуляцією
, сторони якого нескінченно малі, а напрямок його обходу - за годинниковою стрілкою. Циркуляцією 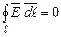 .
. .
. і
і 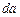 . Тоді другий і четвертий доданки стають рівними нулю і вираз набуває вигляду:
. Тоді другий і четвертий доданки стають рівними нулю і вираз набуває вигляду: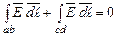
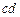 рівні нескінченно малій величині ділянки контуру
рівні нескінченно малій величині ділянки контуру  , в кожній точці якого можна вважати
, в кожній точці якого можна вважати  . Тоді:
. Тоді: ,
, та
та  – вектори напруженості електричного поля на поверхні розподілу першого і другого середовищ відповідно. При цьому:
– вектори напруженості електричного поля на поверхні розподілу першого і другого середовищ відповідно. При цьому:
 , одержимо:
, одержимо: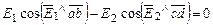 .
.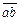 і
і  протилежно спрямовані. Розглядаючи одержану рівність, можна побачити, що перший доданок є не що інше, як тангенціальна складова
протилежно спрямовані. Розглядаючи одержану рівність, можна побачити, що перший доданок є не що інше, як тангенціальна складова  , а інший – тангенційна складова
, а інший – тангенційна складова  . Тоді гранична умова для тангенціальних складових виглядає як:
. Тоді гранична умова для тангенціальних складових виглядає як: ,
, , (1.31)
, (1.31) перетинає границю поділу двох середовищ з параметрами
перетинає границю поділу двох середовищ з параметрами  ,
, – сумарний заряд;
– сумарний заряд; 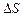 – одиниця площі цієї поверхні. Відповідно до рівності Гауса–Остроградського потік вектора
– одиниця площі цієї поверхні. Відповідно до рівності Гауса–Остроградського потік вектора 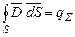 .
.
 , а верхньої –
, а верхньої –  . Твірна циліндра паралельна нормалі
. Твірна циліндра паралельна нормалі  . На площадці
. На площадці 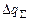 . Тоді потік вектора
. Тоді потік вектора 

 .Очевидно, перший доданок характеризує вектор
.Очевидно, перший доданок характеризує вектор  . При цьому
. При цьому
 ,
, ; другий – нормальна складова
; другий – нормальна складова  . При переході від
. При переході від  до
до  знак в останньому виразі змінюється на протилежний, оскільки векторні площадки
знак в останньому виразі змінюється на протилежний, оскільки векторні площадки  протилежно напрямлені. Тоді гранична умова для нормальних складових вектора
протилежно напрямлені. Тоді гранична умова для нормальних складових вектора 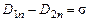 . (1.32)
. (1.32)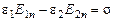 . (1.33)
. (1.33) , а
, а 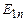 і
і 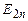 будуть різними внаслідок нерівності
будуть різними внаслідок нерівності  .
.


