
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення та побудова алгебр Лі і асоціативних алгебрСтр 1 из 5Следующая ⇒
Василевич Оксана Вікторівна Науковий керівник: кандидат фізико-математичних наук, асистент Білун С. В.
Київ - 2012 р. Зміст Вступ…………………………………………………………………………………………………... ст. 3
Розділ 1. Основні поняття. …………………………………………………………………. ст. 4 1. 1. Визначення та побудова алгебр Лі і асоціативних алгебр ……..… ст. 4 1. 2. Алгебри лінійних перетворень. Диференціювання…………………....ст. 5 1. 3. Ідеали, розв’язність, нільпотентність……………………………………..….ст. 6 1. 4. Приклади………………………………………………………………………………...…..ст. 8
Розділ 2. Напівпрості алгебри Лі………………………………………………………… ст.9 2. 1. Представлення алгебри. Форми Кіллінга…….…………………………… ст. 9 2. 2. Підалгебри Картана і розклад по кореневим підпросторам….... ст. 10 2. 3. Напівпрості алгебри Лі……………………………………………………….……. ст. 112. 4. Розклад по кореневим підпросторам……………………………………..…ст.12 2. 5. 𝛼 – послідовність ваг………………………………………………………………….ст.13 2. 6. Фундаментальна система коренів і 𝜋 – система……………………… ст. 13 2. 7. Класифікація 𝜋 – систем…………………………………………………………... ст. 15 2. 8. Класифікація простих алгебр Лі. Класичні прості алгебри Лі…. ст. 17
Висновок…………………………………………………………………………………………. ст. 23
Список використаної літератури …………………………………………………… ст. 24
Вступ Теорія алгебр Лі виросла із теорії Лі неперервних груп. Основним результатом останньої є зведення «локальних» задач, що відносяться до груп Лі, до відповідних задач теорії алгебр Лі, тобто до задач лінійної алгебри. Кожній групі Лі співставляється алгебра Лі над полем дійсних або комплексних чисел, і встановлюється відповідність між ана-літичними підгрупами групи Лі і підалгебрами її алгебри Лі, при якому інваріантним підгрупам відповідають ідеали, абелевим підгрупам – абелеві підалгебри і т. д. Ізоморфізм алгебр Лі еквівалентний локальному ізоморфізму відповідних груп Лі. Останнім часом введення відповідних алгебр Лі виявилося корисним при вивченні двох інших розділів теорії груп. Першим із цих розділів є теорія вільних груп, яку можна вивчити за допомогою вільних алгебр Лі. Хоча цей зв'язок не такий тісний, як в теорії Лі, застосування алгебр Лі привело до важливих результатів відносно вільних груп і інших класів абстрактних груп. Варто сказати, що важливу роль в цих застосуваннях до теорії абстрактних груп грають алгебри Лі простої характеристики.
Перший розділ даної роботи присвячений основним поняттям теорії алгебр Лі. Наприкінці нього наведені деякі приклади задач із даної теми. У другому ж розділі розглядаються безпосередньо напівпрості алгебри Лі. Наприкінці підбитий підсумок роботи, також наведений список використаної літератури. Дана робота буде цікава математикам різних спеціальностей та студентам університету. Розділ 1 Основні поняття Приклади 1. Довестипершу та другувластивості закону композиції [𝕭1𝕭2] (3). Доведення: 1. [𝕭1 𝕭2] = 2. [𝕭1 + 𝕭2, 𝕭3] = = 2. Нехай 𝕬, 𝕭 – асоціативні алгебри. Показати, що якщо 𝛉 –гомоморфізм алгебри 𝕬 в 𝕭, то 𝛉 є гомоморфізмом алгебри 𝕬𝐿 в 𝕭𝐿. Доведення: 𝛉 – гомоморфізм алгебри 𝕬 в 𝕭 ⟹ для операцій «−» та «×», визначених на даних алгебрах для ∀ 𝑎1 ∈ 𝕬, 𝑏1 ∈ 𝕭 виконується: 𝛉 (𝑎1 − 𝑏1) = 𝛉 (𝑎1) – 𝛉 (𝑏1); 𝛉(𝑎1 × 𝑏1 ) = 𝛉 (𝑎1) × 𝛉(𝑏1) ⟹ ∀ 𝑎2 ∈ 𝕬𝐿, 𝑏2 ∈ 𝕭𝐿 𝛉 ([𝑎2 𝑏2]) = 𝛉 (𝑎2𝑏2 − 𝑏2𝑎2) = 𝛉 (𝑎2𝑏2) – 𝛉 (𝑏2𝑎2) = 𝛉 (𝑎2) × 𝛉 (𝑏2) − 𝛉(𝑏2) × ×𝛉 (𝑎2) =[ 𝛉 (𝑎2) 𝛉 (𝑏2)] ∎ 3. Якщо 𝑆 – підмножина в лієвій алгебрі 𝕷, то централізатором 𝕮(𝑆) є підмножина таких елементів 𝑐, що [𝑠𝑐]=0 для всіх 𝑠 ∈ 𝑆. Показати, що 𝕮(𝑆) – підалгебра. Доведення: включення очевидне, доведемо замкненість. ∀ 𝑐 ∈ 𝕮(𝑆) [𝑠𝑐] = 𝑠𝑐 − 𝑐𝑠 = 0 ⟹ 𝑠𝑐 = 𝑐𝑠 ⟹ ∀ 𝑐1, 𝑐2 ∈ 𝕮(𝑆) [𝑠,𝑐1𝑐2] = 𝑠𝑐1𝑐2 − 𝑐1𝑐2𝑠 = = 𝑐1𝑠𝑐2− 𝑐1𝑐2𝑠 = 𝑐1𝑐2𝑠 − 𝑐1𝑐2𝑠 = 0. ∎
4. Перевірити, що якщо 𝕷 має базис (е1, е2, …, е8) з таблицею множення [𝑒1 𝑒2] = 𝑒5, [𝑒1 𝑒3] = 𝑒6, [𝑒1 𝑒4] = 𝑒7, [𝑒1 𝑒5] = −𝑒8, [𝑒2 𝑒3] = 𝑒8, [𝑒2 𝑒4] = 𝑒6, [𝑒2 𝑒6] = −𝑒7, [𝑒3 𝑒4] = −𝑒5, [𝑒3 𝑒5] = −𝑒7, [𝑒4 𝑒6] = −𝑒8, всі решта [𝑒𝑖 𝑒𝑗] = 0, і для 𝑖 < 𝑗 [𝑒𝑖 𝑒𝑖] = 0, [𝑒𝑖 𝑒𝑗] = −[𝑒𝑗 𝑒𝑖], то 𝕷 – нільпотентна алгебра Лі. Доведення: Нехай (α,𝑒): = α1𝑒1 + α2𝑒2 + … + α8𝑒8 ∈ 𝕷, де α – деякий скаляр. При піднесенні даного елемента до квадрату ми отримаємо елемент виду β5𝑒5 + β6𝑒6 + β7𝑒7 + β8𝑒8. Знову підносимо до квадрату, в результаті чого отримуємо 0. Отже, дана алгебра Лі 𝕷 є нільпотентною з ступенем нільпотентності 3. ∎
Розділ 2 Напівпрості алгебри Лі Наша перша ціль – показати, що алгебра Лі над полем характеристики 0 напівпроста тоді і тільки тоді, коли вона не вироджена. З огляду на теорему 2. 1. 2., можна звести вивчення напівпростих алгебр Лі до вивчення простих алгебр Лі. На протязі всього цього розділу вважається, що основне поле Р має характеристику 0. Напівпрості алгебри Лі Нехай 𝐿 – алгебра Лі над 𝑃 = (1) 𝐿 = 𝐿 (0) ⨁ 𝐿 (𝛼1) ⨁ … ⨁ 𝐿 (𝛼𝑘) - її розклад на кореневі підпростори відносно підалгебри Картана 𝐿(0)=𝐿0. Нехай 𝑉 – векторний простір над 𝑃 і (𝑉, 𝑓) – представлення алгебри 𝐿. Так як відображення 𝐿0 ∋ 𝑋 ↦ 𝑓 (𝑋) ∈ 𝑔𝑙 (𝑉) є представленням нільпотентної алгебри Лі, то ми отримуємо розклад підпростору 𝑉 в пряму суму (2) 𝑉 = 𝑉 (𝜆1) ⨁ 𝑉(𝜆2) ⨁ …, де 𝜆𝑖 (𝑖 = 1, 2, …) - функції із 𝐿0 в 𝑃 і для довільного 𝑋 ∈ 𝐿0 підпростір 𝑉 (𝜆𝑖) міститься в узагальненому власному підпросторі ендоморфізма 𝑓(𝑋), що відповідає власному значенню 𝜆𝑖 (𝑋). Функції 𝛼1, 𝛼2, …, 𝜆1, …, лінійні; функції 𝜆𝑖 називаються вагами алгебри 𝐿 відносно підалгебри Картана 𝐿0 (і представлення (𝑉, 𝑓)). Розуміється, функції 𝛼1, …, 𝛼𝑘 можна вважати попарно різними, тому існує такий елемент 𝑋 ∈ 𝐿0, що всі числа 𝛼𝑖 (𝑋) відмінні від нуля і від один одного. При такому виборі 𝑋 підпростори 𝐿(𝛼𝑖) співпадають з узагальненими власними підпросторами ендоморфізма 𝑎𝑑 𝑋, що відповідають власним значенням 𝛼𝑖 (𝑋). Звідси, [𝐿 (𝛼𝑖), 𝐿 (𝛼𝑗)] міститься в власному підпросторі, що відповідає власному значенню 𝛼𝑖 (𝑋) + 𝛼𝑗 (𝑋)тобто в 𝐿 (𝛼𝑖 + 𝛼𝑗). Таким чином (3) [𝐿 (𝛼), 𝐿 (𝛽)] ⊂ 𝐿 (𝛼 + 𝛽), де 𝛼, 𝛽 - корені (або 0). Аналогічні міркування дають (4) 𝐿 (𝛼) 𝑉 (𝜆) ⊂ 𝑉 (𝛼 + 𝜆). В (3) і (4) як і раніше мається на увазі, що 𝐿 (𝛼 + 𝛽) = 0, якщо 𝛼 + 𝛽 (≠ 0) не є коренем, і 𝑉 (𝛼 + 𝜆) = 0, якщо 𝛼 + 𝜆 не є вагою. Теорема 2. 3. 1. Нехай 𝐿 – напівпроста алгебра Лі над 𝑃. 1) 𝐿 розкладається в пряму суму простих ідеалів, причому цей розклад однозначний з точністю до порядку доданків. 2) Ідеали і факторалгебри алгебри 𝐿 напівпрості.
3) 𝐿 = 𝐿(1) 4) Алгебра 𝐿 – повна. 5) Для довільного розширення Нехай 𝐿 – алгебра Лі. Довільна підалгебра 𝐴 в 𝐿, інваріантна відносно всіх диференціювань алгебри 𝐿: 𝑑𝑒𝑟(𝐿) 𝐴 ⊂ 𝐴, називається характеристичною. Характеристичні підалгебри є ідеалами. Для довільних 𝑋, 𝑌 ∈ 𝐿 і 𝛿 ∈ 𝑑𝑒𝑟 (𝐿) 𝛿 [𝑋, 𝑌] = [𝛿𝑋, 𝑌] + [𝑋, 𝛿𝑌], і тому 𝐿(1) – характеристична підалгебра. Твердження 2. 3. 2. Радикал є характеристичною підалгеброю.
Висновок Основним результатом роботи є твердження про те, що алгебра Лі над полем характеристики 0 напівпроста тоді і тільки тоді, коли вона невироджена. Це дозволяє звести вивчення напівпростих алгебр Лі до вивчення простих алгебр Лі. Як наслідок отримується ще один важливий результат, а саме - класифікація простих алгебр Лі над полем характеристики 0.
Василевич Оксана Вікторівна Науковий керівник: кандидат фізико-математичних наук, асистент Білун С. В.
Київ - 2012 р. Зміст Вступ…………………………………………………………………………………………………... ст. 3
Розділ 1. Основні поняття. …………………………………………………………………. ст. 4 1. 1. Визначення та побудова алгебр Лі і асоціативних алгебр ……..… ст. 4 1. 2. Алгебри лінійних перетворень. Диференціювання…………………....ст. 5 1. 3. Ідеали, розв’язність, нільпотентність……………………………………..….ст. 6 1. 4. Приклади………………………………………………………………………………...…..ст. 8
Розділ 2. Напівпрості алгебри Лі………………………………………………………… ст.9 2. 1. Представлення алгебри. Форми Кіллінга…….…………………………… ст. 9 2. 2. Підалгебри Картана і розклад по кореневим підпросторам….... ст. 10 2. 3. Напівпрості алгебри Лі……………………………………………………….……. ст. 112. 4. Розклад по кореневим підпросторам……………………………………..…ст.12 2. 5. 𝛼 – послідовність ваг………………………………………………………………….ст.13 2. 6. Фундаментальна система коренів і 𝜋 – система……………………… ст. 13 2. 7. Класифікація 𝜋 – систем…………………………………………………………... ст. 15 2. 8. Класифікація простих алгебр Лі. Класичні прості алгебри Лі…. ст. 17
Висновок…………………………………………………………………………………………. ст. 23
Список використаної літератури …………………………………………………… ст. 24
Вступ
Теорія алгебр Лі виросла із теорії Лі неперервних груп. Основним результатом останньої є зведення «локальних» задач, що відносяться до груп Лі, до відповідних задач теорії алгебр Лі, тобто до задач лінійної алгебри. Кожній групі Лі співставляється алгебра Лі над полем дійсних або комплексних чисел, і встановлюється відповідність між ана-літичними підгрупами групи Лі і підалгебрами її алгебри Лі, при якому інваріантним підгрупам відповідають ідеали, абелевим підгрупам – абелеві підалгебри і т. д. Ізоморфізм алгебр Лі еквівалентний локальному ізоморфізму відповідних груп Лі. Останнім часом введення відповідних алгебр Лі виявилося корисним при вивченні двох інших розділів теорії груп. Першим із цих розділів є теорія вільних груп, яку можна вивчити за допомогою вільних алгебр Лі. Хоча цей зв'язок не такий тісний, як в теорії Лі, застосування алгебр Лі привело до важливих результатів відносно вільних груп і інших класів абстрактних груп. Варто сказати, що важливу роль в цих застосуваннях до теорії абстрактних груп грають алгебри Лі простої характеристики. Перший розділ даної роботи присвячений основним поняттям теорії алгебр Лі. Наприкінці нього наведені деякі приклади задач із даної теми. У другому ж розділі розглядаються безпосередньо напівпрості алгебри Лі. Наприкінці підбитий підсумок роботи, також наведений список використаної літератури. Дана робота буде цікава математикам різних спеціальностей та студентам університету. Розділ 1 Основні поняття Визначення та побудова алгебр Лі і асоціативних алгебр Нагадаємо означення алгебри (не обов’язково асоціативної) (х1 + х2) у = х1у + х2у, х (у1 + у2) = ху1 (1) α (xy) = (αx) y = x (αy), α Аналогічно визначається алгебра над комутативним кільцем Ф, що має одиницю 1. Це лівий Ф -модуль з добутком xy Є Твердження 1. 1. 2. Для асоціативності алгебри 𝔄 з базисом (е1, е2,…, еn) над
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.63.90 (0.043 с.) |
 =
= 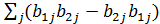 = −
= −  = −[𝕭2 𝕭1].
= −[𝕭2 𝕭1]. =
=  =
=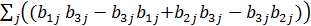 = [𝕭1 𝕭3] + [𝕭2 𝕭3].
= [𝕭1 𝕭3] + [𝕭2 𝕭3]. , і нехай
, і нехай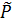 поля 𝑃 алгебра
поля 𝑃 алгебра  напівпроста.
напівпроста.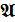 над полем Ф. Це просто векторний простір
над полем Ф. Це просто векторний простір  (2)
(2) , де
, де  ,
,  Ці
Ці 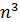 елементів
елементів 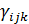 називаються структурними константами алгебри (відносно вибраного базису). Вони дають значення кожного добутку еiеj,
називаються структурними константами алгебри (відносно вибраного базису). Вони дають значення кожного добутку еiеj,  . Більш того, ці константи визначають кожен добуток в 𝔄. Означення 1. 1. 1. Алгебра 𝔄 називається асоціативною, якщо її операція множення задовольняє умові асоціативності (xy) z = x (yz). Алгебра 𝔄 називається алгеброю Лі, якщо її операція множення задовольняє умовам x2 = 0, (xy) z + (yz) x +(zx) y = 0. Друга із цих умов називається тотожністю Якобі.
. Більш того, ці константи визначають кожен добуток в 𝔄. Означення 1. 1. 1. Алгебра 𝔄 називається асоціативною, якщо її операція множення задовольняє умові асоціативності (xy) z = x (yz). Алгебра 𝔄 називається алгеброю Лі, якщо її операція множення задовольняє умовам x2 = 0, (xy) z + (yz) x +(zx) y = 0. Друга із цих умов називається тотожністю Якобі. необхідно і достатньо, щоб виконувалися умови
необхідно і достатньо, щоб виконувалися умови  )
)  =
=  ,
, 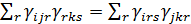 ,
,  , де
, де 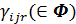 - структурні константи базису (е1, е2, …, еn) алгебри 𝔄: еiеj=
- структурні константи базису (е1, е2, …, еn) алгебри 𝔄: еiеj=  . Алгебра 𝔄 є алгеброю Лі в тому і тільки в тому випадку, коли
. Алгебра 𝔄 є алгеброю Лі в тому і тільки в тому випадку, коли  ,
,  для
для  . В термінах структурних констант ці умови виражаються наступним чином:
. В термінах структурних констант ці умови виражаються наступним чином: .
.


