
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула интегрирования по частям для определённого интеграла.
Теорема 3.15 Пусть функции
Замечание 3.5 Заметим, что эту формулу можно записать в виде
где выражение
называется внеинтегральным членом. Введя обозначения
Доказательство теоремы 3.15. Поскольку из условий теоремы следует, что под знаками интегралов в левой и правой частях равенства стоят непрерывные функции, то к этим интегралам можно применять формулу Ньютона - Лейбница:
и
Пусть
означает, что
где
Но с учётом равенств, полученных выше по формуле Ньютона - Лейбница, это как раз и даёт доказываемую формулу.
Замечание 3.6 Советы, в каких случаях целесообразно применять формулу интегрирования по частям, остаются теми же, как в случае вычисления неопределённых интегралов. Выигрыш от применения формулы интегрирования по частям для определённого интеграла по сравнению с предварительным вычислением первообразной по формуле интегрирования по частям для неопределённого интеграла, а затем применением формулы Ньютона - Лейбница получается от того, что мы сразу, при возникновении внеинтегрального члена, можем вычислить подстановку и далее при преобразованиях использовать полученное число вместо выражения, задающего внеинтегральный член. Пример 3.4 Вычислим интеграл
Выгодно взять
При этом возникший по дороге внеинтегральный член
Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд. Пример 3.5 Вычислим интеграл
применив формулу интегрирования по частям два раза подряд. Имеем:
Если бы мы сразу же не вычисляли значения подстановок во внеинтегральных членах, то нам пришлось бы несколько раз при нахождении первообразных выписывать значения этих внеинтегральных членов
29 Вопрос. Несобственные интегралы первого рода (Определения, примеры). Несобственные интегралы 10.2 Несобственные интегралы 2 рода Определенный интеграл I =∫ baf (x) dx был построен в предположении, что числа a, b конечны и f (x) - непрерывная функция. Если одно из этих предположений нарушается, говорят о несобственных интегралах.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.006 с.) |
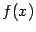 и
и 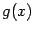 имеют на отрезке
имеют на отрезке 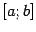 непрерывные производные
непрерывные производные  и
и  . Тогда имеет место формула
. Тогда имеет место формула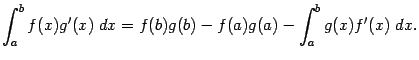
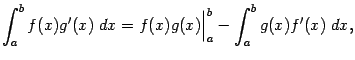
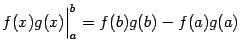
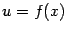 и
и  , мы можем переписать формулу интегрирования по частям в более коротком виде:
, мы можем переписать формулу интегрирования по частям в более коротком виде:
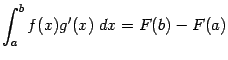

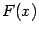 -- некоторая первообразная для функции
-- некоторая первообразная для функции  , а
, а  -- некоторая первообразная для функции
-- некоторая первообразная для функции 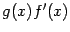 . Формула интегрирования по частям для неопределённого интеграла, то есть
. Формула интегрирования по частям для неопределённого интеграла, то есть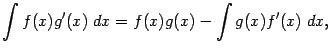

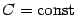 . Положим теперь
. Положим теперь  и
и 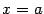 и получим:
и получим: 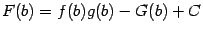 и
и 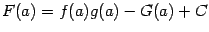 , откуда
, откуда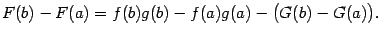
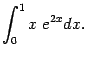
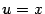 и
и 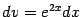 , так что получаем:
, так что получаем: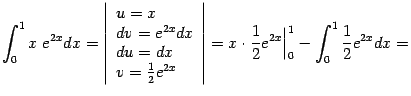
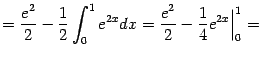

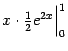 мы вычислили так:
мы вычислили так: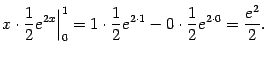

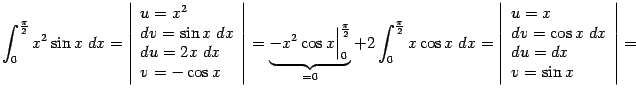
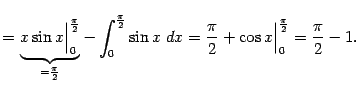
 и
и 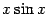 , а здесь мы сразу же заменили первую подстановку на 0, а вторую на
, а здесь мы сразу же заменили первую подстановку на 0, а вторую на 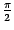 , что сэкономило некоторое место в записи и наши усилия.
, что сэкономило некоторое место в записи и наши усилия.


