
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Аксіоми статики твердого тілаСтр 1 из 6Следующая ⇒
ЗМІСТ
ПЕРЕДМОВА
Автори ставили собі за мету викласти матеріал курсу так, щоб його з найменшим напруженням й на достатньому рівні для подальшого успішного навчання міг би засвоїти будь-який працьовитий студент математичного факультету. Означення, теореми та інші твердження для їх розуміння пояснюються прикладами. Нетривіальні правила для знаходження шуканих величин формулюються у вигляді алгоритмів, тобто у вигляді послідовностей дій для успішного розвязання типових завдань, і ілюструються спеціально підібраними прикладами. Це, на думку авторів, дає змогу студентам «відчути» об’єкти, що вивчаються. Матеріал посібника структуровано таким чином, щоб надати студентам можливість простежити логіку розвитку та взаємозв’язок понять, тверджень та теорем, а також пояснити, як теоретичні конструкції попередніх розділів використовуються у наступних. Враховуючи прикладний характер підготовки студентів, особлива увага приділяється застосуванню теоретичних відомостей до розв’язання практичних задач, вмінню вільно оперувати при цьому вивченими методами. Метою навчальної дисципліни «Додаткові розділи природничих наук» є ознайомлення студентів з базовими поняттями та теоремами статики твердого тіла, а також з методами їх застосування в практичній діяльності людей
Основні завдання: · ознайомити з основними поняттями і теоремами теорії про рівновагу тіл; · забезпечити засвоєння основних методів статики і набуття практичних вмінь і навичок розв’язування основних прикладних задач; · ознайомити з історією розвитку механіки деформівних тіл і з сучасним станом досліджень. У результаті вивчення навчальної дисципліни студент повинен знати: · означення основних понять курсу; · алгоритми розв’язання типових задач; · формулювання основних теорем про рівновагу системи твердих тіл; вміти: · свідомо застосовувати означення, властивості й теореми курсу при розв’язанні теоретичних і практичних питань; · розв’язувати основні типи задач; · обґрунтовувати свої міркування при розв’язанні задач. Доведення наслідку. 4Нехай сила
Згідно з аксіомою 1 система сил АКСІОМА 3 (аксіома паралелограма сил). Дві сили Відзначимо, що одну силу
АКСІОМА 4 (третій закон Ньютона). Сили, з якими два тіла діють одне на одне, рівні за величиною й протилежні за напрямками, лінії дії їх збігаються. Ці сили не утворюють врівноважену систему сил, оскільки прикладені до різних твердих тіл.
Для формулювання ще двох аксіом статики необхідно ознайомитися з поняттям в'язі в механіці. В'язями називають обмеження, які накладаються на переміщення тіла в просторі. У статиці під в'язями розуміють тіла, які перешкоджають даному тілу займати довільне положення в просторі. Сили, з якими в'язі діють на розглядуване тіло, називаються реакціями в'язів. Тіло, на яке не накладені будь-які в'язі, називається вільним. Усі аксіоми статики й засновані на них теореми придатні тільки для вільних тіл. Щоб застосовувати їх до невільних тіл використовується
АКСІОМА 5 (принцип звільнення). Усяке невільне тверде тіло можна вважати вільним, якщо відкинути всі накладені на нього в'язі та замінити їхню дію на тіло відповідними реакціями. АКСІОМА 6 (принцип затвердіння). Якщо нетверде тіло (деформівне тіло) перебуває в рівновазі, то його можна вважати твердим і застосовувати до нього усі аксіоми й теореми статики. Перейдемо тепер до опису реакцій в'язів, які часто зустрічаються на практиці. 1. Ідеально гладка поверхня (поверхня без тертя). Якщо в'яззю для розглядуваного твердого тіла є абсолютно гладка (у механічному та геометричному сенсах) поверхня іншого тіла, то сила реакції такої поверхні (якщо дотик тіл відбувається в одній точці) спрямована по нормалі до цієї поверхні незалежно від того які інші сили прикладені до розглядуваного твердого тіла.
2. Гнучка нерозтяжна нитка (канат, мотузка, трос). Реакція гнучкої нерозтяжної нитки спрямована по дотичній до нитки (у точці з'єднання нитки із твердим тілом) убік відкинутої частини нитки. Цю реакцію називають силою натягу нитки.
3. Ідеальний циліндричний шарнір. Якщо розглядуване тверде тіло шарнірно з’єднано з іншим тілом, тобто може вільно обертатися навколо осі шарніра відносно іншого тіла, то реакція такої в'язі проходить через вісь шарніра і спрямована перпендикулярно осі шарніра.
Зазвичай реакцію циліндричного шарніра розкладають на дві складові за двома заданими напрямками.
4. Рухлива шарнірна опора. Реакція такої опори проходить через вісь шарнірного з'єднання тіла з опорою й спрямована перпендикулярно поверхні, по якій перекочуються циліндри під опорою.
Система сил, прикладених до твердого тіла, називається збіжною, якщо лінії дії всіх сил перетинаються в одній точці. Оскільки в цьому означенні не фігурують розміри твердого тіла, то для зручності теоретичних міркувань його вважають необмеженим. Нехай
Відомо, що точку прикладання сили можна переносити уздовж лінії дії сили (наслідок з аксіом 1 і 2). Тоді вихідну збіжну систему сил можна замінити еквівалентною системою сил, у якій усі сили мають спільну точку прикладання На практиці користуються скалярними умовами рівноваги тіла під дією збіжної системи сил. Для цього вводять у просторі декартову систему координат з осями
Це і є умови рівноваги тіла під дією збіжної системи сил у скалярній формі. Тепер можна сформулювати
ЗАГАЛЬНИЙ ПЛАН РОЗВ'ЯЗАННЯ ЗАДАЧ СТАТИКИ
1. Виділити тіло, рівновагу якого слід розглядати. 2. Звільнити тіло від в'язів, замінивши дію в'язів на тіло реакціями. Зобразити всі сили, прикладені до тіла (включаючи й реакції в'язів). 3. Розумно вибрати декартову систему з осями 4. Скласти рівняння рівноваги тіла ( 5. Розв'язати одержану систему рівнянь і визначити шукані величини.
Розв'язання багатьох задач про рівновагу тіла суттєво полегшує ТЕОРЕМА (про три непаралельні сили). Якщо тверде тіло перебуває в рівновазі під дією трьох сил, лінії дії двох з яких перетинаються, то лінія дії третьої сили проходить через точку перетину ліній дії перших двох сил. Нехай тверде тіло перебуває в рівновазі під дією сил
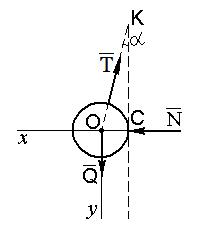
Точки прикладання сил Приклад 1. Визначити силу, з якою залізна куля діє на гладку вертикальну стінку, якщо радіус кулі
Розв'язання. Згідно з планом розв'язання задач статики: 1. Звільнимо кулю від дії мотузки та стінки, замінимо дію цих в'язів на кулю реакціями. 2. Зобразимо сили, що діють на кулю
3. Введемо декартову систему координат як вказано на рисунку. 4. Складемо рівняння рівноваги кулі, враховуючи, що на кулю діє збіжна система сил (за теоремою про три непаралельні сили)
5. Розв’яжемо систему і отримаємо значення невідомих сил
З трикутника ОКС знайдемо
З тотожності
а потім визначимо
Отже
Приклад 2. Визначити реакції опор балки
Розв'язання. 1. Досліджемо рівновагу балки АВ. 2. Замінимо дію опор на балку їх реакціями
Оскільки балка знаходиться в стані рівноваги під дією трьох сил
3. Введемо декартову систему координат з началом у точці А. З рисунку видно, що 4. Складемо рівняння рівноваги балки, на яку діє збіжна система сил
5. Розв’яжемо систему і отримаємо значення невідомих сил
З трикутника АОВ знайдемо
З тотожності
Таким чином,
Приклад 3. Дві гладкі площини з'єднані під прямим кутом, причому одна з площин утворює кут
Розв'язання. Складемо рівняння рівноваги стрижня. На стрижень діє збіжна система сил
Приклад 4. На кронштейні висить тягар, вага якого Р. Визначити зусилля в стержнях, вважаючи їх невагомими.
Розв'язання. Складемо рівняння рівноваги шарніра В. Кожен стрижень конструкції знаходиться під дією двох сил, прикладених до кінців (вагою стрижнів зневажаємо). Будемо припускати, що стрижень 1 розтягнутий, а стрижень 2 – стиснутий. На шарнір В стрижні діють силами
Рівняння рівноваги шарніра мають вигляд:
З цієї системи рівнянь знаходимо
Доведення 4Нехай дві пари сил Доведемо, що ці пари сил еквівалентні. Оскільки
то
або
Продовжимо лінії дії сил заданих пар до їх перетину в точках А і В й перенесемо сили Тоді з подібності трикутників Аа1а2 і Bb1b2 випливає, що З подібності трикутників Аа1а2 і АDB
а з подібності трикутників АCD і BED
Відповідно до останніх двох виразів одержуємо
Порівнюючи рівності Таким чином, пара Оскільки положення пари
- переносити в будь-яке місце у площині дії пари; - повертати плече пари на будь-який кут у площині дії пари; - змінювати довжину плеча і модулі сил пари так, щоб величина моменту пари при цьому не змінювалась. Дія пари на тверде тіло цілком характеризується її моментом, і щоб задати пару, що лежить у заданій площині, досить задати момент цієї пари. Якій величині при цьому дорівнюють сили пари або її плече і де місце розміщення пари в площині її дії – не є істотним. Теорема 2. Пари сил у просторі еквівалентні, якщо рівні їх моменти. Інакше: дія пари сил на тверде тіло не змінюється від перенесення цієї пари сил у паралельну площину.
Нехай дані дві пари сил Доведення 4Візьмемо в площині II відрізок CD, рівний і паралельний відрізку АВ, і у точках C і D прикладемо дві системи зрівноважених (еквівалентних нулю) сил
Складемо сили
прикладені в точці О перетину діагоналей прямокутника ABCD, рівні за модулем і спрямовані по одній прямій у протилежні боки. Тоді сили Оскільки справедлива рівність
то пара З доведеної теореми випливає, що пару сил, не змінюючи її дії на тіло, можна: - переносити в будь-яку площину, паралельну площині її дії; - змінювати плече і силу пари, не змінюючи при цьому величини моменту пари. Отже, при паралельному перенесенні вектора моменту пари сил у будь-яку точку тіла дія пари сил на тверде тіло не зміниться. Таким чином, момент пари сил є вільний вектор, тобто характеризується тільки модулем і напрямком, а точкою прикладення моменту пари може бути будь-яка точка твердого тіла, на яке діє пара сил. Вектор моменту пари сил визначає всі три її елементи: положення площини дії пари, напрямок обертання і числове значення моменту. Таким чином, механічний вплив у статиці твердого тіла характеризується трьома типами векторів: силою – ковзним вектором, моментом сили відносно точки і парою сил – вільним вектором. Теорема 3. Дві пари, розміщені у площинах, які перетинаються, еквівалентні одній парі з моментом, що дорівнює сумі моментів даних пар. Нехай дві пари сил Доведемо, що дві пари, які діють на тверде тіло, можна замінити однією еквівалентною парою – рівнодіючою парою, яка чинила б на тіло таку саму дію, як і вся система двох пар.
Доведення. 4Приведемо обидві пари до одного спільного плеча АВ, розміщеного на лінії перетину площин I і II. Перетворені у такий спосіб пари позначимо
Склавши за правилом паралелограма сили, прикладені в точках А і В, одержимо
Отже,
і сили
або
тобто теорема доведена: момент еквівалентної пари дорівнює сумі моментів пар, що додаються. 3 Отже, щоб скласти дві пари, що розміщені в площинах, які перетинаються, необхідно скласти їх моменти за правилом паралелограма у будь-якій точці тіла. Помітимо, що отриманий результат справедливий і для пар, розміщених у паралельних площинах і. Зокрема, в одній площині (згідно з теоремою 2 пари, що розміщені в паралельних площинах, попередньо можна перенести в одну площину). Установлене правило складання моментів пар сил називається правилом паралелограма моментів. Згідно з цим правилом можна розв’язати і зворотну задачу, тобто розкласти будь-яку пару сил на дві складові пари. А застосовуючи послідовно правило паралелограма до кожних двох моментів пар, можна будь-яку кількість пар замінити однією, еквівалентною заданій системі пар, - рівнодіючою парою. Нехай дана система
Таким чином, система пар зводиться до однієї пари, момент якої дорівнює векторній (геометричній) сумі моментів усіх пар. Для пар, розміщених в одній площині, правило їх складання формулюється як окремий випадок попереднього: пари, що діють на тверде тіло і розміщені в одній площині, можна звести до однієї пари, алгебраїчний момент якої дорівнює сумі алгебраїчних моментів пар, які складаються, тобто
Так само складаються і пари сил, які розміщені в паралельних площинах, тому що всі ці пари попередньо можна перенести в одну площину. Підіб'ємо підсумок сказаному про систему паралельних сил: довільна система паралельних сил еквівалентна або одній силі, або парі сил. Ознайомимося тепер з поняттям центру ваги тіла й опишемо способи його визначення. Якщо розміри твердого тіла малі в порівнянні з радіусом Землі ( Центр системи паралельних сил ваги всіх малих частинок тіла називають центром ваги тіла. Якщо тіло віднести до декартової системі координат з осями
Тут
На практиці для визначення положення центру ваги тіла користуються такими способами: Спосіб симетрії. Якщо тіло має центр, вісь або площину матеріальної симетрії, то центр ваги такого тіла знаходиться в центрі матеріальної симетрії, на осі матеріальної симетрії або в площині матеріальної симетрії. Дійсно, нехай тіло має площину матеріальної симетрії. Не обмежуючи загальності міркувань, будемо вважати, що ця площина є площиною Приклад 1. Визначити центр тяжіння однорідного колового циліндра радіусу R і висоти h.
Розв’язання. Однорідний коловий циліндр має вісь матеріальної симетрії, яка проходить через центри основ циліндра, та площину матеріальної симетрії, яка проходить через середину висоти паралельно основам. Отже центр тяжіння знаходься одночасно на висоті циліндра та на площині симетрії, тобто на середині висоти.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.216.163 (0.227 с.) |
 прикладена до точки
прикладена до точки  тіла. Нехай
тіла. Нехай  довільно взята інша точка тіла, що лежить на лінії дії сили
довільно взята інша точка тіла, що лежить на лінії дії сили 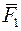 й
й  , рівні за величиною силі
, рівні за величиною силі 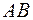 . Сила
. Сила 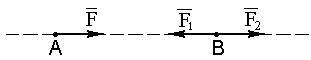
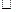 (
(
 , прикладену до деякої точки А тіла, можна замінити сумою двох сил
, прикладену до деякої точки А тіла, можна замінити сумою двох сил 



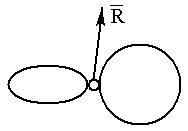


 – збіжна система сил і нехай
– збіжна система сил і нехай  – точка перетину ліній дії сил.
– точка перетину ліній дії сил.
 , прикладені до точки
, прикладені до точки  . Сили
. Сили 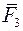 , прикладені до точки
, прикладені до точки  . Продовживши цей процес, замінимо вихідну систему збіжних сил однією силою
. Продовживши цей процес, замінимо вихідну систему збіжних сил однією силою  – її рівнодіючою. Ясно, що тіло буде перебувати в рівновазі під дією збіжної системи сил
– її рівнодіючою. Ясно, що тіло буде перебувати в рівновазі під дією збіжної системи сил 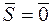 .
. . Рівність нулю вектора
. Рівність нулю вектора 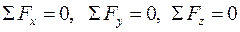 .
. . Нехай лінії дії сил
. Нехай лінії дії сил 
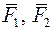 перенесемо в цю точку й після цього замінимо сили
перенесемо в цю точку й після цього замінимо сили  (згідно з аксіомою паралелограма сил). Система трьох сил
(згідно з аксіомою паралелограма сил). Система трьох сил 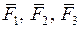 звелася до еквівалентної системи двох сил
звелася до еквівалентної системи двох сил  , під дією яких тіло перебуває в рівновазі. За аксіомою 1 у цьому випадку лінії дії сил повинні збігатися й проходити через їхні точки прикладання. Тому лінія дії сили
, під дією яких тіло перебуває в рівновазі. За аксіомою 1 у цьому випадку лінії дії сил повинні збігатися й проходити через їхні точки прикладання. Тому лінія дії сили  см, вага 30 кГ, довжина мотузки
см, вага 30 кГ, довжина мотузки  см.
см.
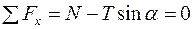 ,
, .
.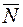 і
і  :
: ,
,  .
. .
. визначимо
визначимо ,
, .
. .
.
 та
та  .
. , то лінії дії цих сил перетинаються в одній точці О (за теоремоюпро три непаралельні сили)
, то лінії дії цих сил перетинаються в одній точці О (за теоремоюпро три непаралельні сили)
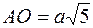 ,
,  ,
,  .
.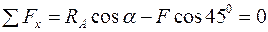 ,
,
 ,
, .
.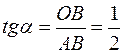 .
. визначимо
визначимо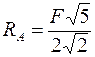 ,
, 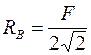 .
. з горизонтом. Знайти кут
з горизонтом. Знайти кут 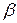 , який утворює з горизонтом важкий стрижень АВ в положенні рівноваги. Кінці стрижня лежать на гладких площинах.
, який утворює з горизонтом важкий стрижень АВ в положенні рівноваги. Кінці стрижня лежать на гладких площинах.
 ,
, 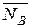 та
та  , тобто сила тяжіння
, тобто сила тяжіння  стрижня та
стрижня та  . Отже,
. Отже,  . Як видно з рисунка,
. Як видно з рисунка,  . Отже,
. Отже, 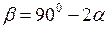 .
.
 і
і 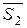 , спрямованими уздовж стрижнів. Таким чином, шарнір В знаходиться в рівновазі під дією збіжної системи сил
, спрямованими уздовж стрижнів. Таким чином, шарнір В знаходиться в рівновазі під дією збіжної системи сил  :
:
 ,
,  .
. ,
, 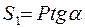
 і
і  розміщені в одній площині з рівними моментами.
розміщені в одній площині з рівними моментами.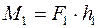 ;
; 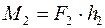 ;
; 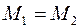 ,
,
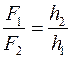 .
. й
й  у ці точки. Відповідно до правила паралелограма розкладемо кожну з цих сил на складові, спрямовані по лінії АВ і лініях дії сил пари
у ці точки. Відповідно до правила паралелограма розкладемо кожну з цих сил на складові, спрямовані по лінії АВ і лініях дії сил пари  і
і  являють собою зрівноважені сили, відкинувши які одержуємо пару
являють собою зрівноважені сили, відкинувши які одержуємо пару  з плечем
з плечем  , яка еквівалентна парі
, яка еквівалентна парі  .
.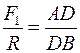 ,
, .
. .
. рівні за модулем силам заданої пари
рівні за модулем силам заданої пари 
 ,
,  і
і  ,
,  , рівних за модулем і паралельних силам пари
, рівних за модулем і паралельних силам пари  .
. ;
; 
 і
і  як зрівноважені можна відкинути. Із зазначеного виходить, що пара
як зрівноважені можна відкинути. Із зазначеного виходить, що пара 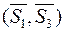 , але розміщеною в паралельній площині II.
, але розміщеною в паралельній площині II. ,
, і
і  мають моменти
мають моменти  і
і 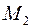 (відповідно) та розміщені у площинах I і II,які перетинаються (див. рисунок нижче). Випадки, коли пари лежать в одній або паралельних площинах, є окремими випадками того, що розглядається.
(відповідно) та розміщені у площинах I і II,які перетинаються (див. рисунок нижче). Випадки, коли пари лежать в одній або паралельних площинах, є окремими випадками того, що розглядається.
 . При цьому повинні виконуватися рівності
. При цьому повинні виконуватися рівності ,
,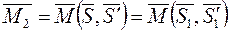 .
.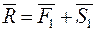 ;
; 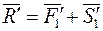 .
.


 ,
, пар
пар  , довільно розміщених у просторі з моментами
, довільно розміщених у просторі з моментами  ,
,  ,...,
,...,  відповідно. Переносячи моменти пар у будь-яку точку О простору і послідовно їх складаючи, можна побудувати многокутник моментів пар, замикаюча сторона якого являє собою момент
відповідно. Переносячи моменти пар у будь-яку точку О простору і послідовно їх складаючи, можна побудувати многокутник моментів пар, замикаюча сторона якого являє собою момент  пари, яка є еквівалентною даній системі пар:
пари, яка є еквівалентною даній системі пар: .
. .
.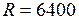 км.), то сили тяжіння його частинок до центру Землі можна практично вважати системою паралельних сил, спрямованих вертикально вниз.
км.), то сили тяжіння його частинок до центру Землі можна практично вважати системою паралельних сил, спрямованих вертикально вниз. можна обчислити за формулами:
можна обчислити за формулами: ,
,  ,
, (3.2)
(3.2) – координати
– координати 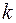 - тої частинки тіла,
- тої частинки тіла, 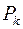 – її вага. Оскільки
– її вага. Оскільки 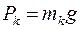 , то у формулах (3.2) сили ваги
, то у формулах (3.2) сили ваги  можна замінити масами частинок
можна замінити масами частинок 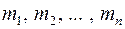 і одержати інші формули для координат центру ваги тіла, більш зручні для застосувань
і одержати інші формули для координат центру ваги тіла, більш зручні для застосувань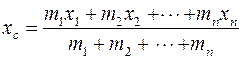 ,
,  ,
, . (3.3)
. (3.3) введеної нами декартової системи координат
введеної нами декартової системи координат  . Це означає, що для кожної частки тіла з координатою
. Це означає, що для кожної частки тіла з координатою  існує така ж частка, симетрично розташована відносно зазначеної площини, яка має таку ж масу як вихідна частка й координату
існує така ж частка, симетрично розташована відносно зазначеної площини, яка має таку ж масу як вихідна частка й координату  . Отже, якщо тіло має площину матеріальної симетрії
. Отже, якщо тіло має площину матеріальної симетрії  , то частці маси
, то частці маси  з координатами
з координатами  , яка не лежить у площині матеріальної симетрії, буде відповідати частка такої ж маси
, яка не лежить у площині матеріальної симетрії, буде відповідати частка такої ж маси  . Якщо ж частка лежить у площині матеріальної симетрії, то її координата
. Якщо ж частка лежить у площині матеріальної симетрії, то її координата  можна розбити на пари, які відповідають симетричним часткам (з координатами
можна розбити на пари, які відповідають симетричним часткам (з координатами  , тобто центр ваги тіла знаходиться в площині матеріальної симетрії тіла. Аналогічно доводяться інші твердження для способу симетрії.
, тобто центр ваги тіла знаходиться в площині матеріальної симетрії тіла. Аналогічно доводяться інші твердження для способу симетрії.



