Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические нагрузки, действующие на ЛА.Стр 1 из 16Следующая ⇒
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КУРСОВОГО ПРОЕКТА ПО КУРСУ «ДИНАМИКА ЛА» (8-9 семестр).
Целью данного методического пособия является научить студента производить оценочные расчеты собственных и вынужденных колебаний ЛА.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ. Динамические нагрузки, действующие на ЛА. (в неустойчивости!?)
Изгибные, продольные, поперечные (крутильные) колебания. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ПРЯМЫХ СТЕРЖНЕЙ Краевые и начальные условия. В простейших случаях, когда конец стержня свободен, или жестко закреплен, или шарнирно оперт, краевые условия выражаются следующими соотношениями: а) конец стержня свободен; на таком конце равны нулю изгибающий момент и поперечная сила; следовательно,
б) конец стержня жестко закреплен; на таком конце равны нулю прогиб и угол поворота, т. е.
в) конец стержня свободно оперт (или закреплен шарниром); в этом случае равны нулю прогиб и изгибающий момент, т.е.
Краевые условия, ограничивающие свободу перемещения концов стержня, называются геометрическими условиями. Таковы, например, условия, в силу которых равны нулю прогиб и угол поворота, т.е. условия
Условия, налагающие ограничения на изгибающий момент и поперечную силу, например, условия, выражающиеся равенствами
мы будем называть динамическими условиями. В других случаях условия закрепления концов стержня выражаются более сложным образом. Например, при упругом закреплении конца стержня соответствующее такому закреплению краевое условие должно учитывать характер возможных смещений конца и возникающих при этом упругих восстанавливающих сил. Так будет, например, в случае закрепления, упругого для поперечных смещений конца и жесткого для поворота или, наоборот, жесткого для поперечных смещений и упругого для поворота и т. д. С такими упругими закреплениями приходится встречаться при расчете на колебания турбинных лопаток, концы которых связаны бандажом, а также при учете упругой податливости заделки хвоста в ободе диска. С некоторыми видами упругих закреплений мы встретимся в разобранных дальше примерах. Отметим, что, оставаясь в пределах линейной теории, мы ограничиваемся рассмотрением краевых условий, выражающихся уравнениями, линейными относительно величин
Начальные условия выражаются соотношениями
имеющими место в момент Рис.6. Факторы, воздействующие на устойчивость двигателя
Факторы, воздействующие на устойчивость двигателя, включают: А- поверхность горения, связывающая давление и скорость газа; В- тепловое излучение; С- вязкоупругие потери в топливе; D- эффекты в камере сгорания, в том числе демпфирующее действие частиц в потоке, другое вязкотермическое затухание, релаксационные затухания, остаточные химические реакции; Е- корпус двигателя, определяющий эффекты вязкотермических потерь на стенках, внешнего влияния и др.; F- эффекты демпфирования сопла. Поверхность горения является источником акустической энергии, а все остальные факторы - ее потерями. Так как неустойчивость возможна до тех пор, пока акустические потерн не превзойдут акустические усиления, то определение акустических потерь отнюдь немаловажно. Представляет интерес знание акустических характеристик зоны горения, которые можно количественно описать удельной акустической проводимостью поверхности горения или передаточной функцией топлива. Характеристики твердого топлива определяются с точки зрения акустики двумя модулями упругости, действительные части которых связаны со скоростью распространения возмущений за счет сдвига и расширения, а мнимые части выражают потери энергии, вызываемые этими возмущениями. Что касается зоны горения, то се толщина существенно меньше по сравнению с сантиметровыми или большими длинами акустических волн, и поэтому ее можно считать принадлежащей поверхности. Это позволяет поверхность горения и другие граничные поверхности камеры характеризовать их акустическими проводимостями, действительная часть которых описывает усиление или затухание акустических колебаний. 3. Теоретическое рассмотрение задачи о высокочастотной неустойчивости требует решения уравнений, описывающих с учетом указанных выше эффектов физические и химические процессы. Эти процессы протекают в объеме, содержащем твердую и газообразную среды, разделенные сложной границей, способной подводить дополнительную энергию в поле акустических колебаний. При этом основным вопросом становится выбор тех форм процесса, на которых следует акцентировать внимание; выбор допущений и упрощений, которые следует сделать при математическом описании модели, с тем, чтобы она была достаточно реальной, поддавалась ясной интерпретации и позволяла математически ее обработать.
На этом пути имеется два направления. Одно - связано с изучением колебаний малой амплитуды на границе устойчивости, а решение задач осуществляется с помощью анализа малых возмущений, приводящего к линейным дифференциальным уравнениям. Основным в линейной теории является вопрос: будет ли расти амплитуда случайных малых возмущений давления, всегда имеющих место в ракетном двигателе или нет. Устойчивость при наличии малых возмущений является необходимым, но не достаточным условием для устойчивости вообще. По этой причине второе направление исследует также колебания с развитой амплитудой, которые описываются нелинейными дифференциальными уравнениями.
Линейный одномерный анализ В любой линейной теории неустойчивости изменение гармонических колебаний во времени изучается с точки зрения того, приводят они к неустойчивости или затухают. Характер переходных процессов в рамках такой теории не исследуется. Вся информация получается путем анализа гармонических колебаний, так как любая функция разлагается на гармонические составляющие. Как известно, в линейной теории рассматриваются колебательные процессы под действием малого начального возмущения. При этом любое возмущение в начальный момент описывается как функция положения в камере сгорания. Для устойчивости необходимо убедиться в затухании всех гармонических составляющих. При анализе же нелинейных эффектов исследовать только гармоническое движение уже недостаточно, так как принцип суперпозиции при этом нарушается. Чтобы найти линейное условие неустойчивости горения, не касаясь вопроса о конечном уровне колебаний, принимают, амплитуду наибольшего возмущения малой. При таком подходе исходные дифференциальные уравнения упрощаются, поскольку величинами второго порядка малости и выше пренебрегают, а анализируются лишь члены, содержащие возмущенные величины в первой степени. Поэтому получаются линейные уравнения относительно возмущений. Линейность возмущений позволяет применить принцип суперпозиции, при котором сумма двух частных решений уравнений также является решением. Поэтому возмущения представляются в виде ряда Фурье, который позволяет анализировать поведение каждого члена ряда в отдельности: при наличии хотя бы одного неустойчивого члена суммарное колебательное движение также будет неустойчивым независимо от поведения остальных членов. Математически это выражается наличием хотя бы одного правого корня в решении характеристического уравнения исходной системы линеаризованных дифференциальных уравнений. При линеаризации исходных уравнений применим несколько отличную по форме от рассматриваемой ранее линеаризации (что одновременно с некоторым упрощением анализа позволяет познакомиться с еще одним методом).
Умножим амплитуду каждого возмущения на
где ε — мера амплитуды давления ~ δр/р°; δp(s) — комплексная амплитуда возмущения давления, при которой действительная часть Определяемые таким образом комплексные амплитуды зависят только от координат точки в пространстве. Возмущения скорости можно представить следующим образом:
где μ - мера амплитуды скорости (среднего числа М); Учитывая сказанное, уравнения (5.63) и (5.64) при помощи отношений (5.69) и (5.70) можно привести к следующему виду:
где В силу того, что ε(μ) малы (но не равны нулю), член в фигурных скобках уравнения (5.71), умножаемый на ε, пропадает, так как появляются слагаемые второго порядка малости. Граничные условия записываются для z = 0 и z = L. Уравнения могут быть решены формально для произвольного движения, но это обычно адекватно рассмотрению только гармонического движения. В результате можно получить ответ на вопрос: будут ли начально малые возмущения возрастать или уменьшаться. В линейном анализе, как выше было указано, используется временная зависимость С учетом принятой временной зависимости
при граничных условиях для z = 0 и z = L
Здесь
Знак (^) относится к амплитудам колебаний далеко от стенки. Совместное рас- смотрение уравнений (5.73), (5.74) и следующих:
позволяет окончательно получить выражение для комплексного волнового числа
где Действительная часть выражения (5.80) определяет искомую величину σ:
(5.82) Здесь Слагаемые, входящие в зависимость (5.82), можно интерпретировать следующим образом. Первый член в фигурных скобках представляет связь с поверхностью горения; первое слагаемое в скобках - для конца заряда, второе - для бокового заряда.
Второй член в фигурных скобках представляет обмен акустической энергией, который связан с массовым потоком через боковую границу; для прихода массы Первое слагаемое третьей фигурной скобки определяет рассеивание акустической энергии вследствие сил взаимодействия между частицами и газом; второе - потери энергии вследствие приобретения акустической энергии частиц через границу. Последний член (5.82) определяет догорание. Отметим, что полученный результат линейного анализа (5.82), позволяет связать общую акустическую энергию в камере ε и 2 σ:
Аналогичные результаты можно получить для трехмерной задачи с более корректной постановкой задачи (без рассмотренных ранее допущений). Подробнее об этом можно найти в работах Ф. Е. Кулика.
Рис. 4.1. Динамическое нагружение топливного образца
Если гармонический закон нагружения представить в комплексной форме записи: ε(t) = εa exp(iωt), а реакцию материала в виде 6(t) = ба ехр [i(ωt +φе)], то их отношение будет иметь вид
Полученное выражение не зависит от времени и является комплексным:
гдe
здесь Частотные характеристики топлива зависят от температуры Т, поэтому их определяют при дискретных температурах в заданном диапазоне эксплуатации изделия. Характерные зависимости для динамического модуля
Рис. 4. 2. Частотные зависимости динамического модуля упругости Е* (а) и угла сдвига фаз фЕ (б): 1- Т=-60°С: 2- (-40°С); 3- (-20°С); 4- (0°С); 5-(20°($ 6- (40°С) Видно, что с ростом частоты и понижением температуры динамический модуль Е* возрастает, а тангенс угла сдвига фаз имеет сложный характер изменения и в сильной степени зависит от состава топлива. Еще одной очень важной характеристикой, определяющей жесткость заряда, является коэффициент Пуассона топлива, равный отношению поперечной деформации образца к продольной при его одноосном растяжении. Специальными исследованиями установлено /19/, что при нагружении твердотопливного образца гармонической продольной деформацией коэффициент Пуассона может иметь динамический смысл
На рис.4.3 приведены характерные для твердого топлива зависимости входящих в выражение (4.3) величин для диапазона частот, представляющего интерес при оценке динамического состояния заряда от действия колебаний давления.
Рис.4.3. Частотные зависимости динамического коэффициента Пуассона м* (а) и угла сдвига фаз фц (б): 1- Т=-бО°С; 2- (-40°С); 3- (-20°С); 4- (0°С): 5- (20°С): б- (40°С); 7- (50°С)
Принцип соответствия В отличие от упругой модели, механические свойства топлива в вязко-упругой модели можно описывать комплексными операторами вязкоупругости - модулем
f = Re [fE exp(iwt)] (4.4) для каждой зависимой переменной, то решение соответствующей задачи для вязкоупругого материала будет иметь вид
где Выражение "соответствующая задача" означает задачу, в которой упругое тело заменено вязкоупругим. Принцип соответствия применим только при следующих условиях: - решение задачи для упругого материала известно; - при решении задачи для упругого материала не применяется операция, которой при решении задачи для вязкоупругого материала будет соответствовать операция отделения действительной (Re) и мнимой (ш) частей комплексного числа, за исключением окончательного определения f; - граничные условия для двух случаев одинаковы. Решения (3.52) - (3.55) для упругих компонентов НДС заряда соответствуют упругой модели (4.4). Для перевода их в вязкоупругую модель (4.5) необходимо в выражениях (3.52) - (3.55) произвести замену упругих характеристик топлива Еn, Проводить непосредственное преобразование выражений (3.52) - (3.55) по указанной схеме нет необходимости, поскольку операция преобразования комплексных выражений успешно решается вычислительной техникой. Рассмотрим некоторые примеры расчетов. Типичные АЧХ и ФЧХ заряда приведены на рис.4.4, где АЧХ: Дбг - относительное контактное радиальное напряжение, Дбг = Дбг / ДР; Де@ - относительная окружная деформация на канале заряда, Д10 = Дев / ДР; ФЧХ: у%- угол сдвига фаз между колебательными составляющими контактного радиального напряжения и давления в камере двигателя. Из рисунка видно, что основной резонанс системы отчетливо проявляется на АЧХ, в то время как второй резонанс настолько слаб, что его можно идентифицировать лишь с помощью ФЧХ. Это еще раз подтверждает, что при радиальных колебаниях основной интерес представляют частотные характеристики основного тона, где, например, динамические напряжения в несколько раз превышают амплитуду осциллирующего давления в камере двигателя. Обычно резонансные пики на АЧХ весьма узкие, так что при некотором удалении от резонансной частоты уровень динамических напряжений и деформаций быстро уменьшается. Это особенно хорошо видно из рис.4.5, где изображены поля относительных динамических напряжений Д6Г= Дбг / ДР, распределенные по своду заряда. Так, для низкомодульного топлива при частоте 140 Гц и угле сдвига фаз фе = 0,1 рад наибольшие напряжения наблюдаются на контактной поверхности, где они усиливаются по сравнению с амплитудой осциллирующего давления более чем в 15 раз. Однако, если частота колебаний давления окажется на 10 Гц больше, контактные напряжения уменьшатся почти вдвое. Такое усиление динамических напряжений в районе основной резонансной частоты объясняется тем, что на поверхности контакта, кроме упругих, действуют инерционные силы, обусловленные движением заряда. В этом заключается основное отличие распределения динамических напряжений 'по своду заряда от квазистатического при действии постоянного давления (рис.4.5, кривая 1). В районе основной резонансной частоты динамические деформации к оболочке уменьшаются. При частотах, близких ко второй и далее формам радиальных колебаний, максимумы динамических напряжений (так же, как и деформаций) смешаются в тело заряда (550 и 940 Гц). Однако величина их всегда намного меньше, чем в районе основного резонанса. Таким образом, расчетным режимом при оценке динамического НДС заряда следует считать основной резонансный или близкий к нему (при Av -» min), а в качестве расчетных выбираются точки на канале для напряжений и окружной деформации и на контакте для напряжений. Эти точки совпадают с аналогичными точками при статическом анализе /5/. поэтому рассчитанные динамические компоненты НДС могут быть учтены при оценке прочности заряда по формулам, приведением в п.1.4.
0 ZOO WO 6O08Off vT/24 Рис.4.4. АЧХ и ФЧХ вязкоупругого заряда: 1- фе = ОД рад; 2- 0,3 рад
Рис.4.5. Поля относительных динамических напряжений: 1- v=0; 2- 140 Гц; 3- 150 Гц; 4- 550 Гц; 5- 940 Гц
Рис.4.13. Схемы разбиения на конечные элементы поперечных сечений заряда Для вынужденной задачи, когда нагрузка изменяется по закону i R > = { Ra }-exp(iu>t), уравнение движения (4.6) принимает вид, аналогичный записи закона Гука: ([ К 1 - и>2-[ М ])•{ 5а > = (4.7) где выражение в круглой скобке описывает динамическую жесткость системы. Индексом "а" обозначены амплитудные значения параметров. Если в уравнении (4.6) принять { Ra > = 0, ш2 = X, то задача сводится к проблеме поиска собственных значений X: (С К 1 - Х'Г М ])•{ ба > = 0. (4.8) Количество собственных значений Xi, а следовательно, и собственных частот колебаний "тределяется размерностью матриц [ К ] и [ М J, которые, в свог. очередь, определяются количеством конечных элементов N. Практическая реализация расчетов МКЭ зависит от конкретного программного обеспечения и без него невозможна /22/. Поэтому для более подробного изучения метода советуем обратиться к соответствующим учебным пособиям и монографиям (например /16,21/ и др.). Здесь же рассмотрим лишь некоторые результаты исследований, позволяющих оценить влияние геометрических особенностей заряда на его динамическое состояние. На рис.4.13 показаны три формы пятилучевого поперечного сечения заряда - щелевая, "звезда" и "вагонное колесо". В табл.4.1 для этих форм приведены результаты расчета первых четырех собственных частот поперечных колебаний заряда по модели плоскодеформированного состояния (ДНО), когда дех = 0. Здесь же приведены амплитудные значения резонансной окружной деформации ueq в расчетных точках 1 и 2 на канале для амплитуды давления ДР = 1 МПа. Таблица 4.1 Динамические параметры зарядов сложной формы
Анализируя полученные результаты, убеждаемся, что сечение сложной формы обладает дополнительной степенью свободы по окружной координате 8. Поэтому колебания из одномерных (только вдоль координаты г) переходят в плоские (в координатной плоскости г - 81, в связи с чем появляются дополнительные собственные частоты в довольно узком диапазоне 130-270 Гц, что является особенностью колебаний сложных сечений. При выгорании топлива происходит сглаживание контура, который постепенно становится близким к окружности. Результаты показывают, что с точки зрения динамики "вагонное колесо" является наименее нагруженным, т.к. при этой форме динамические деформации в расчетных точках имеют наименьшую величину. Поэтому для крупногабаритных двигателей, в которых могут возникнуть продольные колебания газа с частотами 100 - 300 Гц, с точки зрения динамической прочности заряд типа "вагонное колесо" может оказаться наиболее приемлемым. Наибольшую динамическую нагруженностъ могут иметь
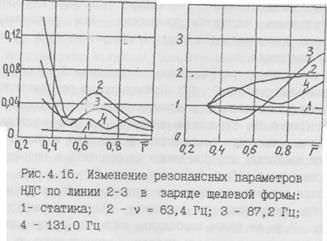
Рис.4.14. Поля динамических деформаций и напряжений по линии 2-3 в заряде типа "вагонное колесо ": 1 - статика; 2 - v = 160 Гц; 3 - 320 Гц На рис.4.14 показаны поля динамических деформаций и напряжений по линии 2-3 в заряде типа "вагонное колесо". Кривые приведены для частот 160 и 320 Гц, соответствующих первым двум продольным модам колебаний газа в канале длиной L = 3,125 м. Видно, что зависимости распределения динамических деформаций и напряжений по своду заряда колебаний гага в канале длиной L = 3,125 м. ьидно, что зависимости распределения динамических деформаций и напряжений по своду заряда имеют сложный характер. По деформации корпуса трудно предположить, что на частоте 320 Гц в теле заряда (г = 0,38) динамическая деформация в 45 раз превышает статическую (Ку = 45), рассчитанную при той же амплитуде давления. Чтобы перевести относительную деформацию ueq МПа"1 в безразмерную величину, как это обычно принято, необходимо знать, какую долю от среднего давления Р0 составляет амплитуда колебаний ДР. Если, например, ДР/Р0 = 0,01, то в указанном сечении динамическая деформация составит 45% от статической. На контактной поверхности наибольший коэффициент динамического усиления по напряжению равен 2,26. Это в несколько раз меньше, чем в случае гладкого цилиндра. Таким образом, в зарядах сложной формы наблюдается "конструкционное демпфирование" - дополнительное снижение уровня динамических напряжений, обусловленное формой заряда. Сравнительные результаты расчетов по одномерной и плоской моделям можно рассмотреть на примере 4- щелевого заряда (R= 1 м, гк = 0,333 м). Так, по модели плоскодеформированного состояния расчетным путем получены собственные частоты 42,2; 63,7; 87,2; 131,2 Гц /23/. Соответствующе АЧХ в расчетных точках 1-4 (по деформации на канале Д1е и по напряжению на контакте Дбг) приведены на рис.4.15.
Рис.4.15. АЧХ в расчетных точках щелевого заряда: 1- точка 1; 2- точка 2; 3- точка 3; 4- точка 4; -----— щелевой канал; - - - - гладкий канал Приведенные на рис.4.14 результаты подтверждают наличие в рассматриваемом диапазоне частот размытой резонансной области, что приводит к необходимости учитывать вязкоупругие потери во всем рассматриваемом частотном диапазоне. Это значительно усложняет анализ при практическом использовании результатов на этапе проектирования двигателя. В то же время рассчитанные по одномерной модели (для гладкого цилиндрического канала) АЧХ вписываются в резонансную область частот и имеют единственную резонансную частоту радиальных колебаний 87,2 Гц (рис.4.15, штриховая кривая). При этой частоте рассчитанные для гладкого цилиндра резонансные деформации и напряжения имеют наибольшую величину, что при учете их значений в расчете идет в запас прочности заряда. Так, например, если ДР = 0,1 МПа, то по одномерной модели резонансные значения окружной деформации на канале и радиального напряжения на контакте будут соответственно 0,025 и 1,1 МПа. В то же время наибольшие значения деформации и напряжения в рассматриваемом диапазоне частот, рассчитанные из условия резонанса по модели плоскодеформированного состояния, соответственно равны 0,02 и 0,3 МПа. Характер изменения динамических деформаций и напряжений в заряде по линии 2-3 на резонансных режимах показан на рис.4.16. Динамические кривые значительно отличаются от статических параметров НДС (кривые 1). Важно отметить, что замеренные в эксперименте деформации корпуса могут дать, согласно расчету (см. рис.4.16), значения, мало отличающиеся по величине от статической деформации при одинаковой величине входного воздействия - внутрикамерного давления. В то же время на канале заряда динамические деформации могут быть существенно выше деформаций, рассчитанных при том же давлении по статической модели. Эту особенность следует учитывать при оценке работоспособности заряда, например, в условиях продольной акустической неустойчивости крупногабаритных РДТТ. Как и для гладкого цилиндрического канала, в районе резонансных частот динамические напряжения в этом случае возрастают к корпусу и имеют наибольшую величину при частоте 87,2 Гц. Другой моделью, используемой для оценки динамического повеления заряда, является модель осисимметричного состояния (ОСС) /22/. когда параметры НДС в окружном направлении 8 не меняются, а зависят только от координат г и х. Для примера на рис.4.17 приведены АЧХ uSa.MfT/T &б>
контактного напряжения в среднем сечении заряда с цилиндрическим каналом длиной L = 3,125 м и наружным радиусом R = 0,5 м для двух значений радиуса канала: гк= 0,2 м - начальное значение; гк= 0,38 м - момент выгорания, когда основная частота радиальных колебаний заряда совпадает с частотой 2-й моды продольных колебаний газа (320 Гц). Расчеты по модели ОСС для начальной геометрии дают резонансную область частот, в которой два пика - при 135 и 200 Гц. По одномерной модели в данной частотной области наблюдается только один радиальный резонанс при частоте 161,6 Гц. При выгорании заряда для рассмотренного среднего сечения различие в АЧХ уменьшается и, например, при гк = 0,38 м (см. рис.4.17) практически исчезает. Резонансная частота по осесимметричной модели равна 319,5 Гц, по одномерной модели - 322,9 Гц. На рис.4.18 представлено изменение амплитуды колебаний относительного радиального напряжения на контакте при частотах 160 Гц (1-я газовая мода, радиус канала в среднем сечении 0,2 м) и 320 Гц (2-я газовая мода, гк = 0,38 м). В заключение отметим, что в динамике сложных форм вместо коэффициента концентрации напряжений, который применяется в статике /4/, более обоснованно использовать понятие коэффициента усиления как отношения динамической компоненты НДС к соответствующей статической, рассчитанной для той же формы заряда при давлении, равном амплитуде колебаний давления в камере. ПРИМЕРЫ РАСЧЕТОВ КОЛЕБАНИЙ. Критерии подобия Опираясь на теорию размерностей и подобия, рассмотрим общую схему построения алгоритма моделирования и создание для этой цели экспериментальной установки. Основные задачи моделирования и создания установки на этом этапе включают: - Анализ факторов и условий работы РДТТ; - Выбор общего математического аппарата, описывающего процессы течения газа в камере сгорания, как натурного, так и модельного двигателя; - Формирование на основании математической модели определяющих параметров и построение базы критериев подобия; - Определение условий моделирования и построение на основе выбранных объектов подобия математического аппарата, позволяющего вести пересчёт полученных результатов на натурный объект; - Выбор рабочего тела и условий его подвода к модельному двигателю; - Моделирование газоприхода с «горящей» поверхности модельного двигателя. Теория подобия является необходимым инструментом всякого экспериментального исследования. Так как для рассматриваемого процесса движение газа в камере сгорания двигателя полное моделирование невозможно, особое значение имеет выбор состава определяющих критериев и оценка их значимости. Такой состав должен обеспечить достаточно полное моделирование основных свойств потока с помощью относительно простых технических решений. Смысл моделирования заключается в том, чтобы дать необходимые ответы о характере эффектов и влиянии различных величин, связанных с явлениями в натурных условиях при формировании течения газа в камере сгорания РДТТ. Из теории подобия следует, что два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчётом, который аналогичен переходу от одной системы единиц измерения к другой, то есть подобными физическими процессами будут такие явления одной природы, которые протекают в геометрически подобных пространственных системах, и, у которых значения переменных, характеризующих одноимённые явления, пропорциональны в сходственных точках и гомохронные моменты времени. Такое преобразование переменных, при котором значение каждой из них меняется в определённое число раз, называется подобным преобразованием. Необходимым и достаточным условием подобия двух явлений является постоянство численных безразмерных комбинаций, образующих базу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.160.216 (0.089 с.) |

 ,
,  ;
; ,
,  ;
;
 ,
,


 где
где  и
и  - некоторые заданные функции переменной
- некоторые заданные функции переменной  , определяющие начальное распределение по оси стержня поперечных отклонений и скоростей отдельных его элементов.
, определяющие начальное распределение по оси стержня поперечных отклонений и скоростей отдельных его элементов. , где
, где 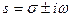 (σ - коэффициент усиления, ω — угловая частота), а возмущение зададим в такой форме:
(σ - коэффициент усиления, ω — угловая частота), а возмущение зададим в такой форме:  ;
; , (5.69)
, (5.69)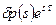 представляет собой действительное мгновенное возмущение (аналогично для плотности).
представляет собой действительное мгновенное возмущение (аналогично для плотности). , (5.70)
, (5.70)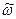 - среднее значение скорости.
- среднее значение скорости.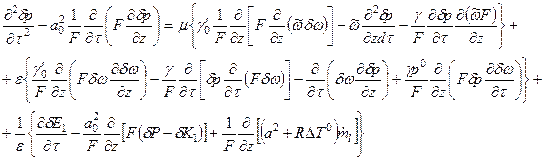 (5.71)
(5.71) , (5.72)
, (5.72)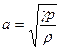 - скорость звука в газе.
- скорость звука в газе.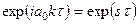 для всех возмущений. Комплексное волновое число k, в котором действительная часть определяет угловую частоту, а мнимая— рост или уменьшение σ, равно:
для всех возмущений. Комплексное волновое число k, в котором действительная часть определяет угловую частоту, а мнимая— рост или уменьшение σ, равно: 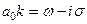 . При σ<0 имеем линейную устойчивость колебаний.
. При σ<0 имеем линейную устойчивость колебаний.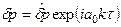 ; (5.73)
; (5.73)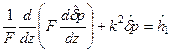 , (5.75)
, (5.75)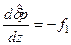 . (5.75)
. (5.75)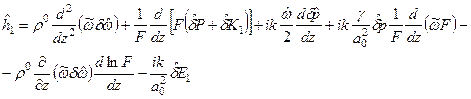 (5.76)
(5.76) . (5.77)
. (5.77)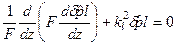 ; (5.78)
; (5.78)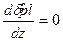 (z =0, L) (5.79)
(z =0, L) (5.79) , (5.80)
, (5.80)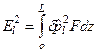 . (5.81)
. (5.81)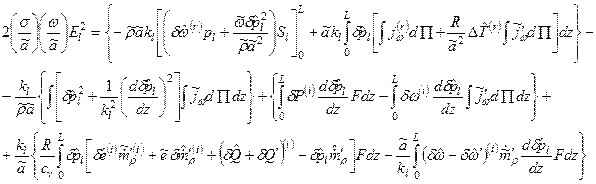
 - приход массы, знак «~» относится к средним величинам.
- приход массы, знак «~» относится к средним величинам.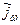 он представляет потери энергии, потому что входящий поток должен приобретать энергию.
он представляет потери энергии, потому что входящий поток должен приобретать энергию. . (5.83)
. (5.83)
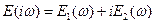


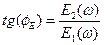
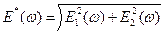
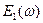 - упругий динамический модуль;
- упругий динамический модуль;  - модуль потерь.
- модуль потерь.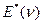 и угла сдвига фаз
и угла сдвига фаз 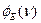 приведены на рис.4.2 /18/.
приведены на рис.4.2 /18/.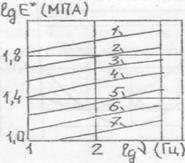

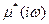 ,т.е. изменяться с частотой нагружения, а между поперечной и продольной деформациями возникает, фазовый сдвиг
,т.е. изменяться с частотой нагружения, а между поперечной и продольной деформациями возникает, фазовый сдвиг 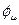 :
: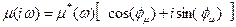 (4.3)
(4.3)

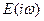 и коэффициентом Пуассона
и коэффициентом Пуассона 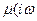 ). Это не единственный способ описания вязкоупругих свойств топлива /17/, но он позволяет наиболее просто получить решение динамической задачи теории линейной вязкоупругости, если известно упругое решение. Для этой цели, при гармоническом нагружении, применяют известный в теории линейной вязкоупругости принцип соответствия /SO/, который формулируется следующим образом: если решение некоторой задачи для упругого материала имеет вид
). Это не единственный способ описания вязкоупругих свойств топлива /17/, но он позволяет наиболее просто получить решение динамической задачи теории линейной вязкоупругости, если известно упругое решение. Для этой цели, при гармоническом нагружении, применяют известный в теории линейной вязкоупругости принцип соответствия /SO/, который формулируется следующим образом: если решение некоторой задачи для упругого материала имеет вид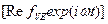 Re
Re  (4.5)
(4.5) обозначает функцию, полученную из функции FЕ заменой упругих постоянных материала на соответствующие комплексные функции.
обозначает функцию, полученную из функции FЕ заменой упругих постоянных материала на соответствующие комплексные функции.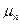 комплексными
комплексными 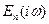 и
и 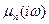 соответственно. Тогда параметры НДС (3.52)-(3.55) также становятся комплексными. После соответствующих алгебраических преобразований по каждой компоненте НДС следует выделить действительную и мнимую часть, после чего определить модуль
соответственно. Тогда параметры НДС (3.52)-(3.55) также становятся комплексными. После соответствующих алгебраических преобразований по каждой компоненте НДС следует выделить действительную и мнимую часть, после чего определить модуль  и аргумент
и аргумент  ) комплексного выражения, т.е. каждое из них представить в виде
) комплексного выражения, т.е. каждое из них представить в виде 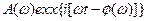 , где А
, где А  - амплитудно-частотная характеристика (АЧХ);
- амплитудно-частотная характеристика (АЧХ); 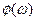 - фазочастотная характеристика (ФЧХ).Знак минус перед ФЧХ обусловлен вязкоупругими свойствами топлива.
- фазочастотная характеристика (ФЧХ).Знак минус перед ФЧХ обусловлен вязкоупругими свойствами топлива.

 заряды типа "звезда".
заряды типа "звезда".