
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Способы проецированияСтр 1 из 11Следующая ⇒
Введение. Начертательная геометрия является основой графической грамотности, необходимой для современного уровня технического творчества. Она развивает логическое мышление и пространственное воображение, способность по плоскому изображению мысленно представлять форму предмета. Начертательная геометрия изучает методы изображения пространственных фигур по чертежу и алгоритмы решения позиционных, метрических и конструкционных задач. Аппаратом начертательной геометрии является чертежно-графическая модель существующих или задуманных предметов реального мира. Изучение начертательной геометрии способствует развитию пространственного воображения, логического мышления, совершенствует способность читать чертежи пространственных форм. Современные инженеры, работающие в различных областях промышленности должны владеть теоретическими основами геометрического моделирования, уметь читать и анализировать чертежи. Знание, умение и навыки, приобретенные при изучение начертательной геометрии необходимы для изучения общеинженерных и специальных технических дисциплин, а также в последующей инженерной деятельности. Данное учебное пособие содержит теоретический материал по начертательной геометрии, контрольные вопросы и задания для самостоятельного решения и демонстрирует возможности использования ПЭВМ для решения ряда задач начертательной геометрии и черчения. Учебное пособие рекомендуется студентам технических вузов направления «Экономика и управление на предприятии» (060800), а также для студентов общетехнических факультетов. Пособие разработано в соответствии с учебной программой по курсу «Основы геометрического моделирования» для специальности 060800 и «Инженерная и машинная графика» для специальностей 210100, 210200. Обозначения и символы
- точки. 1, 2, 3, 4,…
- проекции точек. 11, 21, 31,,… a, b,c, … - прямые линии. (AB) - прямая линия определяемая точками А и В. a1, b1, … (A1B1) - проекции прямых линий. x, y, z - оси координат. p1, p2, p3 - плоскости проекций. S(сигма), T(тау), G(гамма), D(дельта) -плоскости, поверхности. (АВС) - плоскость определяемая точками А, В, С. А1, А2, А3 - объект после последовательных преобразований.
a, b, j - углы. Ç - пересечение. || - параллельность. ^ - перпендикулярность. - скрещивание Ì - взаимная принадлежность объектов (инцидентность) º - совпадение, тождество. ® - логическое следствие. ГЛАВА 1. СПОСОБЫ ПРОЕЦИРОВАНИЯ Центральное проецирование Аппаратом центрального проецирования является плоскость проекции p и центр проецирования точка S, причем S не принадлежит p. Сущность способа в том, что все проецирующие лучи исходят из центра S. Рассмотрим ряд произвольных точек и определим их центральные проекции (рис. 1.2).
Для этого из центра S через точки проведем проецирующие лучи до пересечения с плоскостью проекций. A p и B p– проекции точек А и В на плоскость проекций p. Если для некоторой точки К проецирующий луч оказался параллелен плоскости проекций p, то проекция К p находится в несобственной точке, т.е. К p удалена в бесконечность.
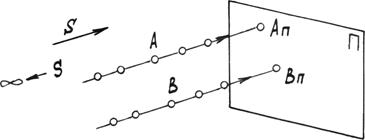
Параллельное проецирование Аппаратом параллельного проецирования является плоскость проекций p и заданное направление проецирования s. Центр проецирования S удален в бесконечность. Сущность способа в том, что все проецирующие лучи параллельны друг другу. Параллельное проецирование является частным случаем центрального проецирования. Определим параллельные проекции точек A и B (рис. 1.3а). Для этого через точки параллельно направлению проецирования проведем проецирующие лучи до пересечения с плоскостью p и найдем проекции точек A p и B p. Обратим внимание, что каждой точке пространства соответствует проекция на плоскости. Однако каждой проекции на плоскости соответствует бесконечное множество точек пространства, т.е. проекция точки на плоскость не определяет ее положение в пространстве.
Для однозначного определения точки в пространстве необходимо иметь два направления проецирования s 1 и s 2 (рис. 1.3б). Тогда две проекции на плоскость A 1p и А 2p однозначно определяют ее положение в пространстве.
ГЛАВА 2. ТОЧКА 2.1. Ортогональная система двух плоскостей проекций.
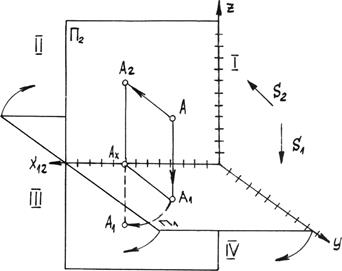
Ортогональное или прямоугольное проецирование является частным случаем параллельного (косоугольного) проецирования. Направление проецирующих лучей в ортогональном проецировании перпендикулярно плоскости проекций. Метод ортогонального проецирования на две взаимно перпендикулярные плоскости носит название метода Монжа. Гаспар Монж (1746 - 1818 г.) – француз, основоположник начертательной геометрии. Зададим две взаимно перпендикулярные плоскости проекций p1 ^ p2 (рис. 2.1) p1 – горизонтальная плоскость проекций, p2 – фронтальная плоскость проекций. Линия пересечения плоскостей называется осью проекций и обозначается х 12.
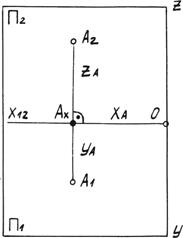
Четыре двухгранных угла, на которые плоскости делят пространство, называются четвертями. Спроецируем точку А, произвольно выбранную в первой четверти, в данной системе плоскостей проекций. Направление лучей проецирования s 1 перпендикулярно p1 и s 2 перпендикулярно p2. А 1 – горизонтальная проекция точки А, А 2 – фронтальная проекция точки А. Проецирующие лучи АА 1 и АА 2 образуют плоскость, которая пересекает плоскость проекций по прямым А х А 1 и А х А 2. Эти прямые перпендикулярны оси x 12 и называются линиями проекционной связи. Повернем плоскость p1 вокруг оси x 12 до совмещения с p2 на 90° в направлении, указанном на чертеже (рис. 2.1). Получим одну плоскость – плоскость чертежа или эпюр (фр. - чертеж) (рис. 2.2).
Эпюром точки называется чертеж, на котором изображены две проекции точки, расположенные в проекционной связи. Две проекции точки вполне определяют ее положение в пространстве. Если из проекции А 1 и А 2 восстановить перпендикуляры к плоскостям проекций, то точка А определится однозначно. Точка А в пространстве определена тремя координатами x, y, z, которые можно измерять на эпюре.
Вопросы и задачи для самоконтроля
Сколько проекций точки вполне определяют ее положение в пространстве? Какая координата точки определяет ее расстояние: a) до горизонтальной плоскости проекций p1; b) до фронтальной плоскости проекций p2; c) до профильной плоскости проекций p3? Выполнить комплексный чертеж точек и указать, в каком октанте они расположены: a) A (x = 50, y = -10, z = -30); b) B (x = -40, y = -20, z = 35); c) C (x = -20, y = -30, z = -45); d) D (x = -30, y = 0, z = -50); e) E (x = 0, y = -40, z = 25). ГЛАВА 3. ПРЯМЫЕ ЛИНИИ Проекции прямой линии Прямая линия в пространстве может быть задана двумя точками. Поэтому эпюр прямой определяется эпюром принадлежащих ей точек. Рассмотрим проекции прямой, заданной отрезком AB (рис. 3.1, 3.2).
А 1 В 1 – горизонтальная проекция прямой;. А 2 В 2 – фронтальная проекция прямой;. А 3 В 3 – профильная проекция прямой. Две проекции прямой вполне определяют ее положение в пространстве. По рис. 3.1 каждая из проекций прямой определяет плоскость, перпендикулярную плоскости проекции (например, А 1 В 1 АВ, А 2 В 2 АВ), которые пересекаются по линии являющейся прямой АВ.
Прямая, определяемая отрезком АВ, непараллельная ни одной из плоскостей проекций и является прямой общего положения. Проекции такой прямой расположены к осям проекций произвольно.
Следы прямой Точка пересечения прямой с плоскостью проекций называется следом прямой. Рассмотрим прямую а общего положения и построим ее следы (рис. 3.10).
Горизонтальный след прямой – это точка пересечения прямой с горизонтальной плоскостью проекций p1. Горизонтальный след обозначается М (М 1, М 2, М 3). Фронтальный след прямой – это точка ее пересечения с фронтальной плоскостью проекций p2. Фронтальный след обозначается N (N 1, N 2, N 3). Профильный след прямой – это точка ее пересечения с профильной плоскостью проекций p3. Профильный след обозначается Р (Р 1, Р 2, Р 3). Следы прямой – это точки частного положения, принадлежащие какой-либо плоскости проекций. Одна из координат = 0.
Из этого следуют правила построения следов: 1. Для построения проекций горизонтального следа необходимо продолжить ее фронтальную проекцию до пересечения с осью х (определяется проекция М 2) и из этой точки восставить перпендикуляр к оси х до пересечения с горизонтальной проекцией прямой (определяется проекция М 1 º М). 2. Для построения проекций фронтального следа необходимо продолжить ее горизонтальную проекцию до пересечения с осью х (определяется точка N 1) и из этой точки восставить перпендикуляр к оси х до пересечения с фронтальной проекцией прямой (определяется точка N 2 º N). 3. Для построения проекций профильного следа необходимо продолжить ее фронтальную проекцию до пересечения с осью z (определяется точка Р 2) и из этой точки восставить перпендикуляр к оси z до пересечения с профильной проекцией прямой (определяется точка P 3 º P). Горизонтальная проекция Р 1 определяется пересечением горизонтальной проекции прямой с осью у.
Вопросы и задачи для самоконтроля Когда след прямой будет находиться в бесконечно удаленной, несобственной точке? Для какой прямой на эпюре следы: a) лежат на оси проекций; b) совпадают. Построить следы прямой, определяемой точками А и В: a) А (10, 20, 50); В (20, 50, 10). b) А (60, 25, 60); В (20, 10, 25). c) А (10, 15, 50); В (50, 15, 10). ГЛАВА 4. ПЛОСКОСТЬ 4.1 Способы задания плоскости Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).
1. Тремя точками, не лежащими на одной прямой (рис. 4.1а). 2. Прямой и точкой вне прямой (рис. 4.1б). 3. Двумя пересекающимися прямыми (рис. 4.1в). 4. Двумя параллельными прямыми (рис. 4.1г). 5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).
6. Следами плоскости (рис. 4.2). Следы плоскости - это линии пересечения плоскости с плоскостями проекций. Линия пересечения плоскости с плоскостью p1 называется горизонтальным следом плоскости Q 1, с плоскостью p2-фронтальным следом Q 2, с плоскостью p3-профильным следом Q 3. Точки пересечения следов на осях проекций называются точками схода следов Q x, Q y, Q z. Отрезки OQ x, OQ y, OQ z, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).
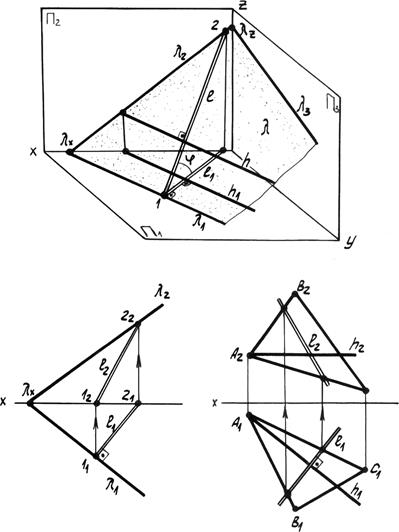
Главные линии плоскости Кроме прямых общего положения в плоскости можно выделить линии частного положения, которые называют главными линиями плоскости – это линии уровня и линии наклона плоскости. 1. Горизонтали плоскости h – прямые, принадлежащие плоскости и параллельные плоскости p1 (рис. 4.6).
На эпюре фронтальная проекция горизонтали h 2 параллельна оси x, а горизонтальная проекция горизонтали h 1 параллельна горизонтальному следу плоскости h 1 || Т1, т.е. горизонтальный след плоскости – это тоже её горизонталь. 2. Фронтали плоскости ¦ – прямые, принадлежащие плоскости и параллельные плоскости p2 (рис. 4.7). На эпюре горизонтальная проекция фронтали ¦1 параллельна оси x 1, а фронтальная проекция фронтали параллельна фронтальному следу плоскости ¦2 || Г2, т.е. фронтальный след плоскости – это тоже фронталь плоскости.
3. Профильные прямые плоскости p – прямые, принадлежащие плоскости и параллельные плоскости p3 (рис. 4.8).
На эпюре горизонтальная и фронтальная проекции профильной прямой р 1 и р 2 перпендикулярны оси x, а профильная проекция профильной прямой р 3 параллельна профильному следу р 3 || q3, т.е. профильный след плоскости – это тоже её профильная прямая. 4. Линия наибольшего наклона плоскости l – это прямая, принадлежащая плоскости и перпендикулярная к соответствующей линии уровня плоскости. С помощью линии наибольшего наклона определяется угол наибольшего наклона плоскости к соответствующей плоскости проекции. Линия l, перпендикулярная горизонтальной плоскости, определяет угол наклона плоскости к плоскости p1 (рис. 4.9). Если плоскость задана следами, то горизонтальная проекция линии наибольшего наклона плоскости перпендикулярна горизонтальному следу l1 (рис. 4.9). Если плоскость задана другим способом, необходимо построить горизонталь плоскости, тогда горизонтальная проекция линии наибольшего наклона определяется перпендикулярно горизонтальной проекции горизонтали, l 1 ^ h 1. Аналогично можно построить линии наибольшего наклона к другим плоскостям проекции.
Параллельные плоскости.
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 4.10). При задании плоскости следами две плоскости параллельны, если параллельны их одноимённые следы (рис. 4.10).
Задача: Через току К провести плоскость параллельную заданной плоскости Т (рис. 4.11).
Решение: Через точку проводим горизонталь h параллельную заданной плоскости Т, т.е. h1 параллельно Т1. Найдём фронтальный след горизонтали N (N1, N2). Через фронтальный след горизонтали N2 проведём фронтальный след искомой плоскости Г2 параллельно фронтальному следу плоскости Т2, определяется точка схода следов Гx. Проводим горизонтальный след плоскости Г1 из Гx параллельно горизонтальному следу Т2. Пересекающиеся плоскости. Две плоскости пересекаются по прямой линии, для построения которой достаточно, или определить две общие для плоскостей точки, или одну точку и направление линии пересечения. Рассмотрим задачи на построение проекций линии пересечения плоскостей и их положения относительно плоскостей проекций. 1. Если плоскости заданы следами и следы пересекаются в пределах чертежа (рис. 4.14а) то, две точки линии пересечения определяются на пересечение одноимённых следов. Точка 1 – пересечение горизонтальных следов, точка 2 – пересечение фронтальных следов. Линия l (1112) - линия пересечения плоскостей l и å.
2. Один из частных случаев пересечения плоскостей, когда одна из них является проецирующей плоскостью (рис. 4.14б). Задача сводиться к определению второй проекции линии, принадлежащей и проецирующей плоскости, и плоскости общего положения. Определяем точки пересечения соответствующего следа проецирующей плоскости с плоскостью общего положения точки 1 и 2. По линиям связи определяем вторую проекцию. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.
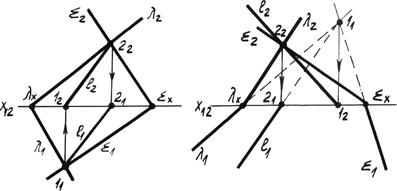
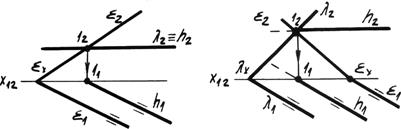
3. В некоторых случаях линия пересечения плоскостей является линией частного положения (рис. 4.14в). Рассмотрим задачи на пересечение плоскостей по горизонтали. В первой задаче одна из плоскостей l является горизонтальной плоскостью уровня, поэтому фронтальная линия проекции пересечения h 2 совпадает со следом этой плоскости и является горизонталью. Горизонтальная проекция определяется по точке 1 пересечения следов и направлению h 1 || l1.
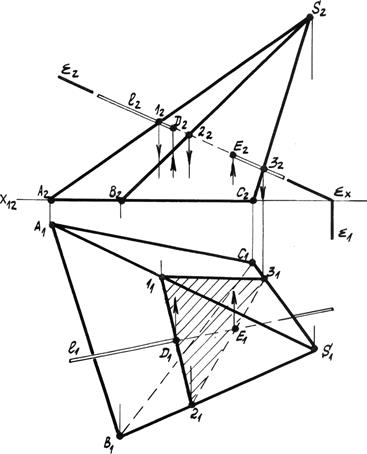
Во второй задаче горизонтальные следы плоскостей общего положения параллельны l1 || å1. Следовательно, горизонтальная проекция линии пересечения будет им параллельна h 1 || l1 || å1, а фронтальная будет проходить через точку 1 пересечения фронтальных следов. Аналогичны случаи пересечения по фронтали. Существуют другие частные случаи пересечения плоскостей, когда линией пересечения являются проецирующие прямые. 4. Общий случай пересечение плоскостей, когда в пределах чертежа сразу не определяются общие для данных плоскостей точки. Для решения такой задачи используются вспомогательные секущие плоскости обычно частного положения – или плоскости уровня, или проецирующие. Рассмотрим пример на рис. 4.15. Даны две плоскости, заданные параллельными прямыми (а || b) и треугольником АВС. Для определения двух общих точек данных плоскостей решаем задачу по алгоритму: 1. Вводим первую вспомогательную горизонтальную плоскость уровня å. 2. Строим линии пересечения каждой данной плоскости со вспомогательной (а || b) Ç å ® h å (ABC) Ç å ® h å. Эти линии являются горизонталями данных плоскостей. 3. Определяем точку пересечения линии пересечения. Точка I – общая для данных плоскостей.
4. Для определения ещё одной общей точки выводим вторую вспомогательную секущую плоскость уровня. l Выполним те же построения и определим вторую общую точку II. 5. Соединяем получившиеся точки I и II, Которые определяют линии пересечения плоскостей l (l 1, l 2). При решении некоторых задач удобнее использовать вспомогательные проецирующие плоскости.
Вопросы и задачи для самоконтроля 1. Какими способами можно задать плоскость на чертеже? 2. Как можно перейти от любого способа задания плоскости к способу задания следами? 3. При каких условиях точка и прямая принадлежат плоскости? 4. Какие прямые линии в плоскости называются главными, и как они направлены? 5. Сформулируйте условия параллельности прямой линии плоскости и условия параллельности плоскостей. 6. Когда прямой угол между прямой линией и плоскостью проецируется в натуральную величину? 7. В каких случаях плоскости пересекаются по линиям частного положения: a) прямыми уровня; b) проецирующими прямыми. 8. Определите линию пересечения двух плоскостей, заданных параллельными прямыми (a || b) и пересекающимися прямыми (c || d) (задать самостоятельно). 9. Определите точку пересечения прямой (общего положения) с плоскостью S (общего положения.) Глава 5. Способы преобразования проекций Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и решение методических и позиционных задач. В итоге при преобразовании чертежа объекты занимают частное положение относительно плоскостей проекций. Существуют несколько способов преобразования. - способ замены плоскостей проекций. - способ вращения вокруг проецирующих прямых и прямых уровня. - способ плоскопараллельного перемещения. Принципиальная разница первого способа (замены плоскостей проекций) в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения – система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей.
Способ вращения Суть способа вращения состоит в том, что геометрический объект вращают в пространстве вокруг выбранной оси i до требуемого положения относительно плоскостей проекций. Траектории движения точек объекта являются дугами окружностей, центр которых находится на оси вращения.
Вопросы и задачи для самоконтроля 1. В чём сущность способа перемещения плоскостей проекций? 2. Сколько нужно выполнить последовательных преобразований и каких, чтобы определить натуральную величину плоскости общего положения? 3. Как движутся точки геометрического объекта при его вращении вокруг осей перпендикулярных плоскостям проекции? 4. Сколько нужно выполнить последовательных вращений и каких, чтобы преобразовать прямую общего положения в проецирующую? 5. Определите расстояние между двумя параллельными прямыми общего положения способом плоскопараллельного перемещения? 6. Определите натуральную величину треугольника вращением вокруг фронтали. ГЛАВА 6. Поверхности Многогранные поверхности Развертка многогранника Разверткой поверхности называется плоская фигура, полученная совмещением поверхности с плоскостью. Построение разверток важно для тех видов производства, где продукция изготавливается из листового материала. При проектировании листовых конструкций выполняется построение разверток их поверхностей. При построении развертки многогранника необходимо определить натуральную величину всех его граней.
Существует несколько способов построения разверток: способ нормального сечения, способ раскатки. Рассмотрим построение развертки призмы способом нормального сечения. Задача: Дана треугольная призма (рис. 6.5). Построить развертку поверхности данной призмы.
Решение: Пересечем призму плоскостью Т перпендикулярно ее боковым ребрам. Полученное сечение (123) называется нормальным. Так как ребра призмы в данной задаче являются горизонталями, то след плоскости нормального сечения Т1 перпендикулярен горизонтальным проекциям ребер A 1 F 1, B 1 D 1, C 1 E 1. Определяем натуральную величину нормального сечения призмы плоскостью Т способом вращения вокруг оси i. Фигура (1 Для построения развертки на горизонтальной линии отложим отрезки, равные сторонам нормального сечения 1020 º 1
Кривые поверхности Основные понятия В начертательной геометрии кривая поверхность определяются, как непрерывное множество положений перемещающейся в пространстве линии, называемой образующей. Образующая может быть прямой линией (линейчатая поверхность) или кривой (нелинейчатая). Движение образующей в пространстве может осуществляться по некоторому закону. Такая поверхность называется закономерной, в отличии от незакономерной (случайной) поверхности. К числу условий перемещения в пространстве образующей линии относятся: перемещение по неподвижным линиям - направляющим, вращательное движение вокруг неподвижной оси, винтовое перемещение и др. Одна и та же поверхность может быть образована перемещением различных линий и согласно различных условиям. Например, боковая поверхность прямого кругового цилиндра может быть рассмотрена как результат: - перемещение окружности вдоль некоторой оси; - вращение некоторой образующей прямой линии вокруг оси вращения; - вращение некоторой кривой линии, все точки которой равноудалены от оси вращения. Рассматривая совокупность прямолинейных образующих с совокупностью образующих окружностей получим каркас данной поверхности цилиндра. Множество неподвижных линий, инцидентных данной поверхности и объединенных каким либо общим признаком, называется её каркасом.
Задание поверхности вращения на чертеже. Точки и линии на поверхности На чертеже поверхность изображают очерком проекций поверхности или её отдельных частей. Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этой поверхности. Точка принадлежит поверхности, если она находится на линии, принадлежащей данной поверхности. Рассмотрим чертёж конуса и точки, принадлежащие его поверхности (рис. 6.6). Фронтальная проекция конуса задана очерковыми образующими, определяющими границы поверхности, а горизонтальная – проекцией основания конуса. Каркас конуса – это совокупность образующих прямых линий, соединяющих их вершину S и основание конуса и совокупность параллелей – окружностей различного радиуса, плоскость которых перпендикулярна оси конуса.
Рассмотрим ряд точек на боковой поверхности конуса. Точка А расположена на очерковой образующей конуса, её горизонтальная проекция находится на линии связи, на оси конуса. Обратим внимание, что очерковая образующая является фронталью, т.е. её фронтальная проекция натуральная величина образующей конуса. Принадлежность точек В и С поверхности конуса определяется соответственно с помощью параллели радиуса R или образующей конуса (S 1).
Вопросы и задачи для самоконтроля 1. Какая поверхность называется многогранником? 2. Перечислите правильные многогранники? 3. Что такое развёртка многогранника, и какие существуют способы её построения? 4. Что называется переносом поверхности? 5. Как определить проекции точки принадлежащие поверхности вращения? 6. При каком расположении секущей плоскости в сечении конуса получаются окружность, парабола, эллипс. гипербола? 7. В чём сущность способов секущих плоскостей и секущих сфер при определении линии пересечении линии пересечения поверхностей вращения? 8. Определите линию пересечения двух конусов с вертикальными осями вращения (конусы задайте самостоятельно). Возможности системы AutoCAD Автоматизация проектирования - неотъемлемая составляющая современного научно-технического прогресса. САПР - процесс проектирования с использованием сложных средств машинной графики, снабженных специальными пакетами программного обеспечения. Достоинства автоматизации проектирования: 1. Сокращение сроков проектирования; 2. Повышение качества и точности чертежей; 3. Возможность многократного использования чертежа; 4. Специальные чертежные средства (графопостроители, принтеры, плоттеры); 5. Интеграция проектирования с другими видами деятельности; 6. Сокращение числа ИТР, занятых проектом, т.к. повышается производительность их труда. Средства САПР можно сгруппировать по видам обеспечения автоматизированного проектирования: 1. Математическое обеспечение САПР - это совокупность алгоритмов, математических моделей и методов. Элементы математического обеспечения САПР чрезвычайно разнообразны. 2. Программное обеспечение представляет собой совокупность всех программ и эксплуатационной документации к ним, необходимых для выполнения автоматизированного проектирования. Программное обеспечение делится на общесистемное и специальное (прикладное). (Пакеты Прикладного Программирования). 3. Аппаратное (техническое) обеспечение - комплекс технических средств. 4. Информационное обеспечение - это базы данных, которыми пользуются проектировщики в процессе проектирования (нормативно--справочная документация, исходные и результирующие данные и т.п.). Различают специальные способы ведения информационного фонда САПР: использование файловой системы, построение библиотек, использование банков данных, создание информационных программ адаптеров. 5. Лингвистическое обеспечение САПР - его основу составляют совокупность языков программирования. 6. Методическое обеспечение - это документы, регламентирующие порядок эксплуатации САПР. 7. Организационное обеспечение - различные положения, инструкции. Основные возможности системы Автокад: - быстрая генерация рисунка; - редактирование чертежа с целью исправления ошибок или внесения изменений; - создание библиотек графических фрагментов; - структурное представление чертежа как совокупности простых и сложных объектов, совокупности слоев; - возможность разработки собственных команд и функций с помощью языка программирования Auto LISP; - удобный вывод чертежей и их фрагментов на устройства получения твердой копии. Изучение системы AutoCAD можно разбить на следующие этапы:
1. Графический редактор поддерживает: - рисование чертежа; - редактирование чертежа; - установку свойств примитивов (тип линии, цвет); - работу с экраном (увеличить/уменьшить, освежить изображение). 2. Работа с внешними устройствами - вывод на принтер, использование дигитайзера, мыши. 3. В Автокаде используются два режима работы: диалоговый и пакетный. Первый режим позволяет в графическом редакторе с помощью стандартного меню команд создавать изображение в диалоге. Второй режим позволяет, используя непосредственно систему команд Автокада, создать файл - пакет команд, после выполнения которых получается изображение на экране. Запустить на выполнение этот пакет команд можно с помощью специальной команды редактора. 4. Автокад можно адаптировать к прикладной области. При необходимости - модифицировать типы линий, создать свои штриховки, создать конфигурированное меню, библиотеки стандартных элементов. Автокад - это оболочка, которую можно начинить и приспособить к любой области проектирования. После входа в графический редактор выглядит следующим образом:
- Основная (центральная) часть отведена под графическую зону (вывод чертежа). По этой части движется перекрестье, показывающее текущее значение координат точки (в центре перекрестья). - В правой части экрана выводится экранное меню верхнего уровня, все команды которого невозможно одновременно разместить в этой ограниченной области. Поэтому экранное меню состоит из множества подменю. Выбор какого-либо пункта меню вызывает появление на экране опций, относящихся к этой строке. - Три строки в нижней части экрана используются для диалога: запросы, ввод команд и данных, подсказки. - Верхняя строка: 1. Строка состояния - текущее состояние режимов, имя слоя, текущие координаты. 2. Вывод "падающего меню" при наведении на верхнюю строку перекрестья.
7.1.1. Манипулятор "Мышь" Манипулятор "Мышь" используется для ускорения ввода команд и точек, выбора графических объектов. "Мышь" имеет 2 или 3 кнопки: левая - указания, правая - ввода. Левой кнопкой можно: - ввести точку в месте расположения перекрестья;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.54 (0.179 с.) |
 A, B, C, D,…
A, B, C, D,…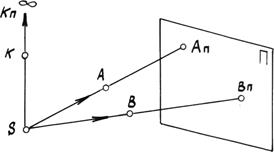


















 2
2 



