
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ньютона (метод касательных).
Суть метода состоит в том, что на
Уравнение касательной, проведенной к кривой
За следующее приближение корня
При этом необходимо, чтобы Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках
Для завершения итерационного процесса можно использовать условия Объем вычислений в методе Ньютона больше, чем в других методах, поскольку приходится находить значение не только функции Пример 1.2. Решить уравнение Решение. Определим первые и вторые производные заданной функции
Аналогично находится второе приближение:
Третье приближение:
Так как На рис. 1.7 приведена программа решения данного уравнения методом Ньютона. В качестве исходных данных вводятся начальное приближение и точность вычисления.
Пример 1.3. Решить уравнение
Порядок решения (рис. 1.8). 1) Ввести в ячейки A1:D1 заголовки столбцов.
2) В ячейку A2 – значение начального приближения 3) В ячейку B3 – формулу функции =A2^3+A2-1 4) В ячейку C3 – формулу производной функции =3*A2^2+1 5) В ячейку A3 – формулу первого приближения =A2-B3/C3 6) В ячейку D3 – погрешность =ABS(A3-A2) 7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения. 8) В столбце A найти значение корня, соответствующее заданной точности. Приближенное решение данного уравнения
Метод простой итерации. Для использования этого метода исходное нелинейное уравнение В качестве
Если известно начальное приближение корня Далее подставляя каждый раз новое значение корня в уравнение
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е. Геометрическая интерпретация метода простой итерации. Построим графики функций
Пример 1.4. Решить уравнение Решение. Из условия сходимости (1.5) Подставляя каждый раз новое значение корня в уравнение
получаем последовательность значений:
Теперь На рис.1.10 приведена программа решения данного уравнения методом простой итерации. В качестве исходных данных вводятся начальное приближение, точность вычисления и значение постоянной М.
Пример 1.4. Решить уравнение
Порядок решения (рис. 1.11). 1) Ввести в ячейки A1:D1 заголовки столбцов. 2) В ячейку A2 – значение начального приближения 3) В ячейку B3 – формулу функции =A2^3+A2-1 4) В ячейку C2 – значение M 5 5) В ячейку A3 – формулу первого приближения =A2-B3/$C$2 6) В ячейку D3 – погрешность =ABS(A3-A2) 7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения. 8) В столбце A найти значение корня, соответствующее заданной точности. Приближенное решение данного уравнения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.166 (0.017 с.) |
 -й итерации в точке
-й итерации в точке  строится касательная к кривой
строится касательная к кривой  и ищется точка пересечения касательной с осью абсцисс (рис. 1.6). Если задан интервал изоляции корня
и ищется точка пересечения касательной с осью абсцисс (рис. 1.6). Если задан интервал изоляции корня 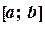 , то за начальное приближение
, то за начальное приближение 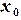 принимается тот конец отрезка, на котором
принимается тот конец отрезка, на котором . (1.1)
. (1.1) с координатами
с координатами  , имеет вид:
, имеет вид: (1.2)
(1.2)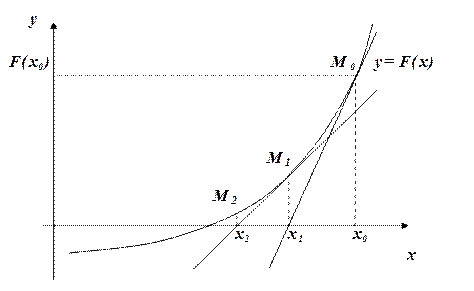
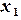 примем абсциссу точки пересечения касательной с ocью OX. Из (1.2) при
примем абсциссу точки пересечения касательной с ocью OX. Из (1.2) при  ,
,  получим
получим (1.3)
(1.3) .
.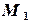 ,
,  и т.д. Формула для
и т.д. Формула для  -го приближения имеет вид:
-го приближения имеет вид: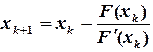 (1.4)
(1.4) или
или  .
.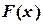 , но и ее производной. Однако скорость сходимости здесь значительно выше.
, но и ее производной. Однако скорость сходимости здесь значительно выше.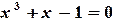 на отрезке
на отрезке 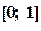 методом Ньютона c точностью
методом Ньютона c точностью 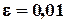 .
. :
:  ;
;  . Проверим выполнение условия сходимости на концах заданного интервала:
. Проверим выполнение условия сходимости на концах заданного интервала:  - не выполняется,
- не выполняется,  - выполняется. За начальное приближение корня можно принять
- выполняется. За начальное приближение корня можно принять 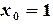 . Находим первое приближение:
. Находим первое приближение: .
. .
. .
. , итерационный процесс заканчивается. Таким образом, приближенным решением данного уравнения является
, итерационный процесс заканчивается. Таким образом, приближенным решением данного уравнения является  .
. с помощью программы Excel.
с помощью программы Excel.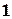
 содержится в ячейке A6 (погрешность
содержится в ячейке A6 (погрешность  в ячейке D6).
в ячейке D6).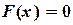 необходимо привести к виду
необходимо привести к виду 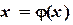 .
.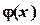 можно принять функцию
можно принять функцию 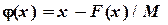 , где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации
, где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации 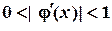 . При этом для определения M условие сходимости записывается в следующем виде:
. При этом для определения M условие сходимости записывается в следующем виде: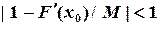 или
или 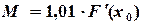 . (1.5)
. (1.5) , подставляя это значение в правую часть уравнения
, подставляя это значение в правую часть уравнения 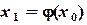 .
. ,
, 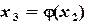 ,...,
,..., 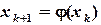 , k = 1,2,...,n.
, k = 1,2,...,n. .
.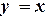 и
и 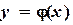 . Корнем
. Корнем 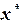 уравнения
уравнения 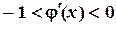 на отрезке
на отрезке  (рис. 1.9б), то последовательные приближения сходятся монотонно.
(рис. 1.9б), то последовательные приближения сходятся монотонно.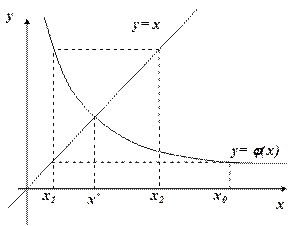

 , при
, при 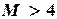 .Пусть
.Пусть 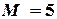 .
.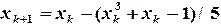 ,
,

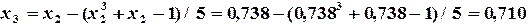
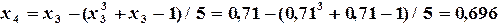
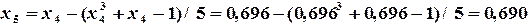
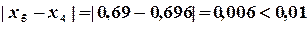 , но
, но 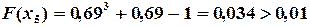 , поэтому продолжаем вычисления.
, поэтому продолжаем вычисления.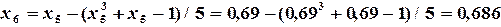
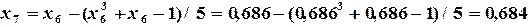
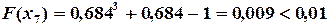 и приближенным решением данного уравнения c точностью
и приближенным решением данного уравнения c точностью 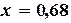 .
. содержится в ячейке A9 (погрешность
содержится в ячейке A9 (погрешность 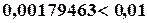 в ячейке D9).
в ячейке D9).


