
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей совместных событий. Формула полной вероятности. Вероятность гипотез. Формулы Байеса. Теорема сложения вероятностей совместных событий.Стр 1 из 2Следующая ⇒
Полная группа событий. Полной группой событий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна Теорема. Сумма вероятностей событий А1, А2,..., Аn, образующих полную группу, равна единице: Р (A1) + Р (А2) +... + Р (Аn) = Противоположные события. "Принцип практической невозможности маловероятных событий": если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит. Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0,01 и 0,05. Уровень значимости, равный 0,01, называют однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным, и т. д. если событие А имеет вероятность, близкую к нулю, то вероятность противоположного события А близка к единице. С другой стороны, непоявление события А означает наступление противоположного события А. Таким образом, из принципа невозможности маловероятных событий вытекает следующее важное для приложений следствие: если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании это событие наступит 4. Условная вероятность - условной вероятностью РА(В)события Вназывается вероятность события В, найденная в предположении, что событие А уже наступило. Обозначается Ра(В) или Р(В/А). Теорема умножения вероятностей: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло Р(АВС…КL)=Р(А)*Ра(В)*Рав(С)…Равс..к(L) Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошло.
Событие В называют независимым от события А, если появления события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности: Pa(B)=P(B); Pb(A)=P(A). Два события называют независимыми, если вероятность их совмещений равна произведению вероятностей этих событий; иначе события "зависимые". "Несколько событий называются независимыми", если каждые два из них независимы. Например события А,В,С попарно независимы, если независимы события А и В, А и С, В и С. "Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*P(B), т.е. вероятность появления двух Теорема умножения вероятностей независимых событий
независимых событий равна произведению вероятностей этих событий. Вероятность появления хотя бы одного события Теорема. Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Формула полной вероятности. ТЕОРЕМА. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2, …, В п, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р(А) = Р(В1)РВ1(А) + Р(В2)РВ2(А) + … Р(В п)РВ п (А) Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий В1, В2, …, В п. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А, …, В п А. Пользуясь для вычисления вероятности события А теоремой сложения, получим Р(А) = Р(В1А) + Р(В2А) + … Р(В п А). (*) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем Р(В1А) = Р(В1)РВ1(А); Р(В2А) = Р(В2)РВ2(А); …; Р(ВпА) = Р(В п)РВ п (А). Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности
Р(А) = Р(В1)РВ1(А) + Р(В2)РВ2(А) + … Р(В п)РВ п (А) Формула Бернули. Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна pkqn-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. C kn. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число: Рn(k) = C knpkqn-k или P n(k)=____ n!____ pkqn-k k!(n-k)! Полученную формулу называют формулой Бернулли. Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р n(k) того, что событие А появиться в n испытаниях ровно k раз, приближенно равна значению функции
при x =(k – np)/ Вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна Pn(k) ≈˜ Серднее квадратическое отклонение. Ср.квадрат-е отклонение суммы взаимно независимых случайных величин.Одинаково распределенные взаимно независимые случайные величины.Начальные и центральные теоретические моменты. Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии. Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин. Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ: Если число измерений примерно равно 10, то истинное значение величины может отличаться от среднего арифметического не более чем на величину среднего квадратичного отклонения σ. Отклонения, большие, чем σ, возможны лишь в исключительных случаях, число которых составляет около 0.5% всех возможных случаев. Если число измерений значительно больше десяти, то максимальное практически возможное отклонение истинной величины от среднего арифметического будет меньше чем σ. Отклонение не превысит значения: ▲=3 σ/ √n. Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в σ (Х) = σ/√n Таким образом, среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина. С увеличением n величина
Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk: Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X—M(X))k: теоретическими. В отличие от теоретических моментов, моменты которые вычисляются по данным наблюдений, называют эмпирическими.
Полная группа событий. Полной группой событий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна Теорема. Сумма вероятностей событий А1, А2,..., Аn, образующих полную группу, равна единице: Р (A1) + Р (А2) +... + Р (Аn) = Противоположные события. "Принцип практической невозможности маловероятных событий": если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит. Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0,01 и 0,05. Уровень значимости, равный 0,01, называют однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным, и т. д. если событие А имеет вероятность, близкую к нулю, то вероятность противоположного события А близка к единице. С другой стороны, непоявление события А означает наступление противоположного события А. Таким образом, из принципа невозможности маловероятных событий вытекает следующее важное для приложений следствие: если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании это событие наступит 4. Условная вероятность - условной вероятностью РА(В)события Вназывается вероятность события В, найденная в предположении, что событие А уже наступило. Обозначается Ра(В) или Р(В/А).
Теорема умножения вероятностей: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло Р(АВС…КL)=Р(А)*Ра(В)*Рав(С)…Равс..к(L) Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошло. Событие В называют независимым от события А, если появления события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности: Pa(B)=P(B); Pb(A)=P(A). Два события называют независимыми, если вероятность их совмещений равна произведению вероятностей этих событий; иначе события "зависимые". "Несколько событий называются независимыми", если каждые два из них независимы. Например события А,В,С попарно независимы, если независимы события А и В, А и С, В и С. "Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*P(B), т.е. вероятность появления двух Теорема умножения вероятностей независимых событий
независимых событий равна произведению вероятностей этих событий. Вероятность появления хотя бы одного события Теорема. Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Теорема сложения вероятностей совместных событий. Формула полной вероятности. Вероятность гипотез. Формулы Байеса. Теорема сложения вероятностей совместных событий. ТЕОРЕМА. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В) = Р(А) + Р(В) – Р(АВ) Доказательство. Поскольку события А и В, по условию, совместны, то событие А+В наступит, если наступит одно из следующих трех несовместных событий: А В, А В или АВ. По теореме сложения вероятностей несовместных событий, Р(А+В) = Р(А В) + Р(А В) + Р(АВ) (*) Событие А произойдет, если наступит одно из двух несовместных событий: А В или АВ. По теореме сложения вероятностей несовместных событий имеем Р(А) = Р(А В) + Р(АВ). Отсюда, Р(А В) = Р(А) – Р(АВ). (**) Аналогично имеем Р(В) = Р(А В) + Р(АВ). Отсюда Р(А В) = Р(В) – Р(АВ). (***) Подставив (**) и (***) в (*), окончательно получим Р(А+В) = Р(А) + Р(В) – Р(АВ) Формула полной вероятности. ТЕОРЕМА. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2, …, В п, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р(А) = Р(В1)РВ1(А) + Р(В2)РВ2(А) + … Р(В п)РВ п (А)
Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий В1, В2, …, В п. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А, …, В п А. Пользуясь для вычисления вероятности события А теоремой сложения, получим Р(А) = Р(В1А) + Р(В2А) + … Р(В п А). (*) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем Р(В1А) = Р(В1)РВ1(А); Р(В2А) = Р(В2)РВ2(А); …; Р(ВпА) = Р(В п)РВ п (А). Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности Р(А) = Р(В1)РВ1(А) + Р(В2)РВ2(А) + … Р(В п)РВ п (А)
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1029; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.48.131 (0.043 с.) |
 Теорема. Сумма вероятностей противоположных событий равна единице:
Теорема. Сумма вероятностей противоположных событий равна единице: 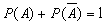 .
.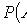
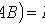
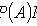
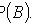 где
где 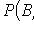
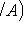 - вероятность события B при условии, что произошло событие A.
- вероятность события B при условии, что произошло событие A.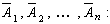 Р (A) = 1 — q 1 q 2... q n.
Р (A) = 1 — q 1 q 2... q n.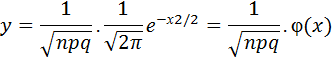
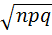 .
.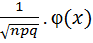 где, x=(k-np)/
где, x=(k-np)/ 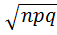 .
.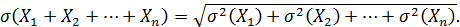
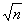 раз меньше среднего квадратического отклонения каждой величины:(Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных и Дисперсия среднего арифметического)
раз меньше среднего квадратического отклонения каждой величины:(Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных и Дисперсия среднего арифметического)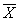 почти перестает быть случайной и приближается к постоянной М. Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений. Начальные и центральные теоретические моменты.
почти перестает быть случайной и приближается к постоянной М. Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений. Начальные и центральные теоретические моменты.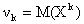
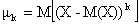 Моменты, рассмотренные здесь, называют
Моменты, рассмотренные здесь, называют


